题目内容
已知f(x)=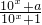 是奇函数.
是奇函数.
(1)求a的值;
(2)求f(x)的反函 数 f-1(x),判断f-1(x)的奇偶性,并给予证明;
(3)若函数y=F(x)是以2为周期的奇函数,当x∈(-1,0)时,F(x)=f-1(x),求x∈(2,3)时F(x)的表达式.
解:(1)∵f(x)=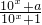 是奇函数,由f(0)=
是奇函数,由f(0)=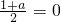 ,得a=-1;
,得a=-1;
(2)由y=f(x)=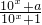 ,
,
得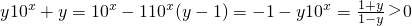 ,
,
∴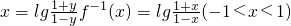 .
.
而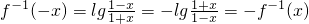 ,
,
∴f-1(x)在(-1,1)上是奇函数;
(3)因为当-1<x<1时,F(x)=f-1(x)
∴当2<x<3时,-3<-x<-2?-3+2<2-x<0?-1<2-x<0
∴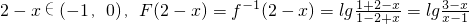 ,
,
又∵F(x)是以2为周期的奇函数,
∴F(2-x)=F(-x)=-F(x)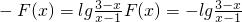
∴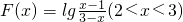 .
.
分析:(1)函数f(x)是定义在实数集上的奇函数,由f(0)=0求解a的值;
(2)由函数解析式利用指数式和对数式的互化求解x,把x和y互换后得到原函数的反函数,然后利用就行的定义证明奇偶性;
(3)由2<x<3两边同时乘以-1,再加2后求出2-x的范围,代入F(x)=f-1(x),再利用周期函数的性质得到x∈(2,3)时F(x)的表达式.
点评:本题考查了函数的性质,考查了函数的反函数的求法,训练了指数式和对数式的互化,通过对定义域的变化求解函数解析式是解答该题的关键,是中档题.
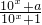 是奇函数,由f(0)=
是奇函数,由f(0)=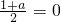 ,得a=-1;
,得a=-1;(2)由y=f(x)=
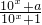 ,
,得
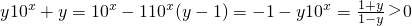 ,
,∴
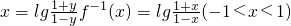 .
.而
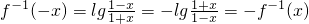 ,
,∴f-1(x)在(-1,1)上是奇函数;
(3)因为当-1<x<1时,F(x)=f-1(x)
∴当2<x<3时,-3<-x<-2?-3+2<2-x<0?-1<2-x<0
∴
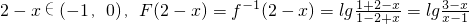 ,
,又∵F(x)是以2为周期的奇函数,
∴F(2-x)=F(-x)=-F(x)
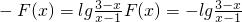
∴
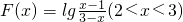 .
.分析:(1)函数f(x)是定义在实数集上的奇函数,由f(0)=0求解a的值;
(2)由函数解析式利用指数式和对数式的互化求解x,把x和y互换后得到原函数的反函数,然后利用就行的定义证明奇偶性;
(3)由2<x<3两边同时乘以-1,再加2后求出2-x的范围,代入F(x)=f-1(x),再利用周期函数的性质得到x∈(2,3)时F(x)的表达式.
点评:本题考查了函数的性质,考查了函数的反函数的求法,训练了指数式和对数式的互化,通过对定义域的变化求解函数解析式是解答该题的关键,是中档题.

练习册系列答案
相关题目
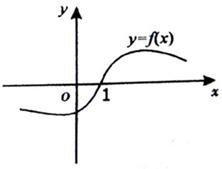 已知函数f(x)(x∈R)的一段图象如图所示,f′(x)是函f(x)(数的导函数,且y=f(x+1)是奇函数,给出以下结论:
已知函数f(x)(x∈R)的一段图象如图所示,f′(x)是函f(x)(数的导函数,且y=f(x+1)是奇函数,给出以下结论: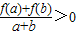 成立.
成立.