题目内容
17.若集合P={x|R|x2<9},Q={1,2,3,4},M={x|R|2x<4},则P∩Q={1,2},P∪M=(-3,2),∁RM=[2,+∞).分析 求出P与M中不等式的解集确定出P与M,找出P与Q的交集,P与M的并集,找出M的补集即可.
解答 解:由P中不等式解得:-3<x<3,即P=(-3,3),
由M中不等式变形得:2x<4=22,即x<2,
∴M=(-∞,2),
∵Q={1,2,3,4},
∴P∩Q={1,2},P∪M=(-3,2),∁RM=[2,+∞),
故答案为:{1,2};(-3,2);[2,+∞)
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
7.已知集合A={-2,-1,1,2},B={x|x2+x-2>0},则A∩(∁UB)=( )
| A. | {-2,-1,1} | B. | {-1,1,2} | C. | {-1} | D. | {1} |
5.设集合A={x|x2-3x-4<0},B={x|x>1},则A∩B=( )
| A. | (1,4) | B. | (-1,1) | C. | (1,+∞) | D. | (-1,+∞) |
2.已知函数f(x)=lnx-($\frac{1}{2}$)x-2的零点为x0,则x0所在的区间是( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
7.某学校开设“蓝天工程博览课程”,组织6个年级的学生外出参观包括甲博物馆在内的6个博物馆,每个年级任选一个博物馆参观,则有且只有两个年级选择甲博物馆的方案有( )
| A. | $A_6^2×A_5^4$种 | B. | $A_6^2×{5^4}$种 | C. | $C_6^2×A_5^4$种 | D. | $C_6^2×{5^4}$种 |
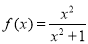 ,则
,则 等于( )
等于( )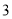 B.
B.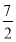
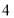 D.
D.