题目内容
两个变量之间的线性相关程度越低,则其线性相关系数的数值( )
| A.越小 | B.越接近于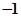 | C.越接近于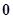 | D.越接近于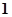 |
C
解析试题分析:因为两个变量之间的线性相关程度越低,其线性相关系数的数值越接近于0即选C.
考点:变量的相关性.

练习册系列答案
相关题目
某医疗研究所为了检验新开发的流感疫苗对甲型H1N1流感的预防作用,把1000名注射了疫苗的人与另外1000名未注射疫苗的人的半年的感冒记录作比较,提出假设H0:“这种疫苗不能起到预防甲型H1N1流感的作用”,并计算出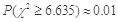 ,则下列说法正确的( )
,则下列说法正确的( )
| A.这种疫苗能起到预防甲型H1N1流感的有效率为1% |
| B.若某人未使用该疫苗,则他在半年中有99%的可能性得甲型H1N1 |
| C.有1%的把握认为“这种疫苗能起到预防甲型H1N1流感的作用” |
| D.有99%的把握认为“这种疫苗能起到预防甲型H1N1流感的作用” |
对四组数据进行统计,获得以下散点图,关于其相关系数的比较,正确的是( ).
| A.r2<r4<0<r3<r1 | B.r4<r2<0<r1<r3 | C.r4<r2<0<r3<r1 | D.r2<r4<0<r1<r3 |
已知某高中高一800名学生某次考试的数学成绩,现在想知道不低于120分,90~
120分,75~90分,60~75分,60分以下的学生分别占多少,需要做的工作是( )
| A.抽取样本,据样本估计总体 | B.求平均成绩 |
| C.进行频率分布 | D.计算方差 |
设某大学的女生体重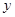 (单位:
(单位: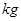 )与身高
)与身高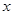 (单位:
(单位: )具有线性相关关系,根据一组样本数据
)具有线性相关关系,根据一组样本数据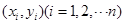 ,用最小二乘法建立的回归方程为
,用最小二乘法建立的回归方程为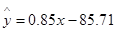 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A.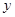 与 与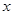 具有正的线性相关关系 具有正的线性相关关系 |
B.回归直线过样本点的中心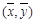 |
| C.若该大学某女生身高增加lcm,则其体重约增加0.85kg |
| D.若该大学某女生身高为170cm,则可断定其体重必为58.79kg |
某产品的广告费用x与销售额y的统计数据如表:
| 广告费用x(万元) | 4 | 2 | 3 | 5 |
| 销售额y(万元) | 49 | 26 | 39 | 54 |
根据上表可得回归方程
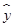 =
= x+
x+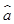 中的
中的 为9.4,据此模型预报广告费用为6万元时销售额为( )
为9.4,据此模型预报广告费用为6万元时销售额为( )A.63.6万元 B.65.5万元 C.67.7万元 D.72.0万元
为了了解某地参加计算机水平测试的1000名学生的成绩,从中随机抽取200名学生进行统计分析,分析的结果用下图的频率分布直方图表示,则估计在这1000名学生中成绩小于80分的人数约有( )
| A.100人 | B.200人 | C.300人 | D.400人 |
 (件)与销售价格
(件)与销售价格 (元/件)负相关,则其回归方程可能是( )
(元/件)负相关,则其回归方程可能是( )



 的总体抽取容量为
的总体抽取容量为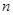 的样本,当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时,总体中每个个体被抽中的概率分别为
的样本,当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时,总体中每个个体被抽中的概率分别为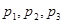 ,则( )
,则( )


