题目内容
设某大学的女生体重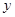 (单位:
(单位: )与身高
)与身高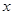 (单位:
(单位: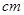 )具有线性相关关系,根据一组样本数据
)具有线性相关关系,根据一组样本数据 ,用最小二乘法建立的回归方程为
,用最小二乘法建立的回归方程为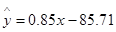 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A.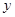 与 与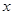 具有正的线性相关关系 具有正的线性相关关系 |
B.回归直线过样本点的中心 |
| C.若该大学某女生身高增加lcm,则其体重约增加0.85kg |
| D.若该大学某女生身高为170cm,则可断定其体重必为58.79kg |
D.
解析试题分析:根据回归方程为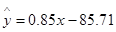 知,
知,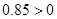 ,所以
,所以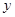 与
与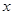 具有正的线性相关关系,故
具有正的线性相关关系,故 正确;又因为回归直线过样本点的中心
正确;又因为回归直线过样本点的中心 ,故
,故 正确;因为
正确;因为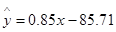 ,所以该大学某女生身高增加lcm,则其体重约增加0.85kg,故
,所以该大学某女生身高增加lcm,则其体重约增加0.85kg,故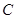 正确;当
正确;当 时,
时,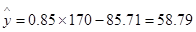 ,但这是预测值,不可断定其体重为58.79kg,故
,但这是预测值,不可断定其体重为58.79kg,故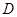 不正确.
不正确.
考点:回归分析的初步应用.

某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本.若样本中的中年职工为5人,则样本容量为( )
| A.7 | B.15 | C.25 | D.35 |
某医疗研究所为了检验某种血清预防感冒的作用,把500名使用血清的人与另外500名未使用血清的人一年中的感冒记录作比较,提出假设H:“这种血清不能起到预防感冒的作用”,利用2×2列联表计算的K2≈3.918,经查临界值表知P(K2≥3.841)≈0.05.则下列表述中正确的是( )
| A.有95℅的把握认为“这种血清能起到预防感冒的作用” |
| B.若有人未使用该血清,那么他一年中有95℅的可能性得感冒 |
| C.这种血清预防感冒的有效率为95℅ |
| D.这种血清预防感冒的有效率为5℅ |
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,一般情况下PM2.5的浓度越大,大气环境质量越差.右边的茎叶图表示的是成都市区甲乙两个监测站某10日内每天的PM2.5浓度读数(单位: ),则下列说法正确的是( )
),则下列说法正确的是( )
| A.这10日内甲、乙监测站读数的极差相等 |
| B.这10日内甲、乙监测站读数的中位数中,乙的较大 |
| C.这10日内乙监测站读数的众数与中位数相等 |
| D.这10日内甲、乙监测站读数的平均数相等 |

在2014年3月15日,某超市对某种商品的销售量及其售价进行调查分析,发现售价x元和销售量y件之间的一组数据如下表所示:
| 售价x | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y | 11 | 10 | 8 | 6 | 5 |
由散点图可知,销售量y与售价x之间有较好的线性相关关系,其线性回归方程是:y= -3.2x+a,则a=( )
A.-24 B.35.6 C.40.5 D.40
两个变量之间的线性相关程度越低,则其线性相关系数的数值( )
| A.越小 | B.越接近于 | C.越接近于 | D.越接近于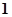 |
为了调查某班级的作业完成的情况,将该班级的52名学生随机编号,用系统抽样的方法抽取一个容量为4的样本,已知5号、31号、44号同学在样本中,那么样本中还有一位同学的编号应该是( )
| A.13 | B.17 | C.18 | D.21 |
为了解儿子身高与父亲身高的关系,随机抽取了5对父子身高数据如下:
| 父亲身高x(cm) | 174 | 176 | 176 | 176 | 178 |
| 儿子身高y(cm) | 175 | 175 | 176 | 177 | 177 |
y对x的线性回归方程为( ).
A.
 B.
B. C.
C. D.
D.