Question

【题目】如图，在四棱锥P﹣ABCD中，底面ABCD是边长为4的正方形，PA⊥平面ABCD，E为PB中点，PB=4 ．

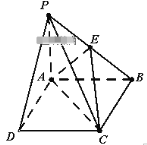
（I）求证：PD∥面ACE；

（Ⅱ）求三棱锥E﹣ABC的体积。

Answer 1

【答案】（1）见解析； （2）.

【解析】

（I）连接BD，交AC于F，连接EF，证明EF∥PD，利用线面平行的判定定理，可得结论；（II）取AB中点为G，连接EG，证明EG⊥平面ABCD，即可求三棱锥E﹣ABC的体积．

（I）证明：连接BD，交AC于F，连接EF．

∵四边形ABCD为正方形

∴F为BD的中点

∵E为PB的中点，

∴EF∥PD

又∵PD面 ACE，EF面ACE，

∴PD∥平面ACE …（5分）

（Ⅱ）解：取AB中点为G，连接EG

∵E为AB的中点

∴EG∥PA

∵PA⊥平面ABCD，

∴EG⊥平面ABCD，

在Rt△PAB中，PB=4，AB=4，则PA=4，EG=2

∴