题目内容
【题目】在直角坐标系xOy中,曲线C的参数方程为 ![]() (θ为参数).以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系.
(θ为参数).以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系.
(1)写出曲线C的极坐标方程;
(2)设点M的极坐标为( ![]() ),过点M的直线l与曲线C相交于A,B两点,若|MA|=2|MB|,求AB的弦长.
),过点M的直线l与曲线C相交于A,B两点,若|MA|=2|MB|,求AB的弦长.
【答案】
(1)解:∵曲线C的参数方程为 ![]() (θ为参数).
(θ为参数).
∴曲线C的直角坐标方程为x2+y2﹣4y=0,
∴曲线C的极坐标方程为ρ2﹣4ρsinθ=0,
即曲线C的极坐标方程为ρ=4sinθ
(2)解:设直线l的参数方程是 ![]() (θ为参数)①
(θ为参数)①
曲线C的直角坐标方程是x2+y2﹣4y=0,②
①②联立,得t2+2(cosθ﹣sinθ)t﹣2=0,
∴t1t2=﹣2,且|MA|=2|NB|,∴t1=﹣2t2,
则t1=2,t2=﹣1或t1=﹣2,t2=1,
∴|AB的弦长AB|=|t1﹣t2|=3
【解析】(1)由曲线C的参数方程先求出曲线C的直角坐标方程,由此能求出曲线C的极坐标方程.(2)先求出直线l的参数方程,与曲线C的直角坐标方程联立,得t2+2(cosθ﹣sinθ)t﹣2=0,由此能求出AB的弦长.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案【题目】某学校课题组为了研究学生的数学成绩与学生细心程度的关系,在本校随机调查了100名学生进行研究.研究结果表明:在数学成绩及格的60名学生中有45人比较细心,另15人比较粗心;在数学成绩不及格的40名学生中有10人比较细心,另30人比较粗心.
(1)试根据上述数据完成2×2列联表;
数学成绩及格 | 数学成绩不及格 | 合计 | |
比较细心 | |||
比较粗心 | |||
合计 |
(2)能否在犯错误的概率不超过0.001的前提下认为学生的数学成绩与细心程度有关系. 参考数据:独立检验随机变量K2的临界值参考表:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() (其中n=a+b+c+d)
(其中n=a+b+c+d)
【题目】某品牌新款夏装即将上市,为了对夏装进行合理定价,在该地区的三家连锁店各进行了两天试销售,得到如下数据:
连锁店 | A店 | B店 | C店 | |||
售价x(元) | 80 | 86 | 82 | 88 | 84 | 90 |
销售量y(件) | 88 | 78 | 85 | 75 | 82 | 66 |
(1)以三家连锁店分别的平均售价和平均销量为散点,求出售价与销量的回归直线方程 ![]() ;
;
(2)在大量投入市场后,销售量与单价仍然服从(1)中的关系,且该夏装成本价为40元/件,为使该款夏装在销售上获得最大利润,该款夏装的单价应定为多少元(保留整数)? 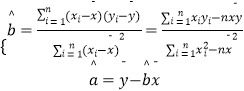 .
.