题目内容
已知函数f(x)=-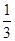 x3+
x3+ x2-2x(a∈R).
x2-2x(a∈R).
(1)当a=3时,求函数f(x)的单调区间;
(2)若对于任意x∈[1,+∞)都有f′(x)<2(a-1)成立,求实数a的取值范围;
(3)若过点 可作函数y=f(x)图象的三条不同切线,求实数a的取值范围.
可作函数y=f(x)图象的三条不同切线,求实数a的取值范围.
(1) 增区间为(1,2),减区间为(-∞,1)和(2,+∞). (2) (-1,8); (3) (2,+∞).
解析试题分析:(1)当a=3时,f(x)=-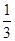 x3+
x3+ x2-2x,得f′(x)=-x2+3x-2.
x2-2x,得f′(x)=-x2+3x-2.
因为f′(x)=-x2+3x-2=-(x-1)(x-2),
所以当1<x<2时,f′(x)>0,函数f(x)单调递增;
当x<1或x>2时,f′(x)<0,函数f(x)单调递减.
故函数f(x)的单调递增区间为(1,2),单调递减区间为(-∞,1)和(2,+∞).
(2)方法一:由f(x)=-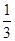 x3+
x3+ x2-2x,得f′(x)=-x2+ax-2.
x2-2x,得f′(x)=-x2+ax-2.
因为对于任意x∈[1,+∞)都有f′(x)<2(a-1)成立,
即对于任意x∈[1,+∞)都有-x2+ax-2<2(a-1)成立,即对于任意x∈[1,+∞)都有x2-ax+2a>0成立.
令h(x)=x2-ax+2a,
要使h(x)对任意x∈[1,+∞)都有h(x)>0成立,必须满足Δ<0,或
即a2-8a<0或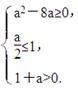 所以实数a的取值范围为(-1,8).
所以实数a的取值范围为(-1,8).
方法二:由f(x)=-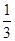 x3+
x3+ x2-2x,得f′(x)=-x2+ax-2.
x2-2x,得f′(x)=-x2+ax-2.
因为对于任意x∈[1,+∞)都有f′(x)<2(a-1)成立,即对于任意x∈[1,+∞)都有f′(x)max<2(a-1).
因为f′(x)=- 2+
2+ -2,其图象开口向下,对称轴为x=
-2,其图象开口向下,对称轴为x= .
.
①当 <1,即a<2时,f′(x)在[1,+∞)上单调递减,所以f′(x)max=f′(1)=a-3.
<1,即a<2时,f′(x)在[1,+∞)上单调递减,所以f′(x)max=f′(1)=a-3.
由a-3<2(a-1),得a>-1,此时-1<a<2;
②当 ≥1,即a≥2时,f′(x)在
≥1,即a≥2时,f′(x)在 上单调递增,在
上单调递增,在 上单调递减,所以f′(x)max=f′
上单调递减,所以f′(x)max=f′ =
= -2.由
-2.由 -2<2(a-1),得0<a<8,此时2≤a<8.
-2<2(a-1),得0<a<8,此时2≤a<8.
综上①②可得,实数a的取值范围为(-1,8).
(3)设点P 是函数y=f(x)图象上的切点,则过点P的切线的斜率为k=f′(t)=-t2+at-2,所以过点P的切线方程为y+
是函数y=f(x)图象上的切点,则过点P的切线的斜率为k=f′(t)=-t2+at-2,所以过点P的切线方程为y+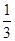 t3-
t3- t2+2t=(-t2+at-2)(x-t).
t2+2t=(-t2+at-2)(x-t).
因为点 在切线上,所以-
在切线上,所以-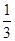 +
+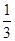 t3-
t3- t2+2t=(-t2+at-2)(0-t),即
t2+2t=(-t2+at-2)(0-t),即 t3-
t3- at2+
at2+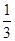 =0.
=0.
若过点 可作函数y=f(x)图象的三条不同切线,则方程
可作函数y=f(x)图象的三条不同切线,则方程 t3-
t3- at2+
at2+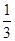 =0有三个不同的实数解.
=0有三个不同的实数解.
令g(t)= t3-
t3- at2+
at2+ ,则函数y=g(t)与t轴有三个不同的交点.
,则函数y=g(t)与t轴有三个不同的交点.
令g′(t)=2t2-at=0,解得t=0或t=
因为g(0)=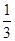 ,g
,g =-
=- a3+
a3+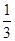 ,所以g
,所以g =-
=- a3+
a3+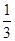 <0,即a>2.
<0,即a>2.
所以实数a的取值范围为(2,+∞).
考点:导数的几何意义;利用导数研究函数的单调性;二次函数的性质;
点评:我们要灵活应用导数的几何意义求曲线的切线方程,尤其要注意切点这个特殊点,充分利用切点即在曲线方程上,又在切线方程上,切点处的导数等于切线的斜率这些条件列出方程组求解。做本题时我们要注意在某点处的切线方程和过某点的切线方程的区别。

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 )图像上一个最高点坐标为(2,2
)图像上一个最高点坐标为(2,2 ),这个最高点到相邻最低点的图像与x轴交于点(5,0).
),这个最高点到相邻最低点的图像与x轴交于点(5,0).
 .
. 在点
在点 处的切线方程;
处的切线方程; 为曲线
为曲线 的切线,且经过原点,求直线
的切线,且经过原点,求直线 的方程及切点坐标
的方程及切点坐标 .
. 奇偶性, 并求出函数
奇偶性, 并求出函数 的单调区间;
的单调区间;  有零点,求实数
有零点,求实数 的取值范围.
的取值范围.

 恒成立?若存在,求出a的取值条件;
恒成立?若存在,求出a的取值条件;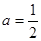 时,求证:f(1)+f(2)+f(3)+…+
时,求证:f(1)+f(2)+f(3)+…+ .
. ,
, 的单调递减区间;
的单调递减区间; 上的最大值为20,求它在该区间的最小值
上的最大值为20,求它在该区间的最小值 
 ,判断函数在定义域内的单调性;
,判断函数在定义域内的单调性; 内存在极值,求实数m的取值范围。
内存在极值,求实数m的取值范围。 的图象经过点M(1,4),曲线在点M处的切线恰好与直线
的图象经过点M(1,4),曲线在点M处的切线恰好与直线 垂直。
垂直。 的值;
的值; 在区间
在区间 上单调递增,求
上单调递增,求 的取值范围.
的取值范围. ,
, ,求函数
,求函数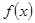 的极小值,
的极小值, ,设
,设 ,函数
,函数 .若存在
.若存在 使得
使得 成立,求
成立,求 的取值范围.
的取值范围.