题目内容
定义在R上的奇函数f(x)满足:①在[-1,1]上的解析式为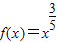 ;②函数f(x+1)是偶函数,则f(2010)的值是( )
;②函数f(x+1)是偶函数,则f(2010)的值是( )A.-1
B.0
C.1
D.
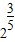
【答案】分析:利用函数奇偶性进行转化确定函数的进一步性质是解决本题的关键:可以确定出函数的周期为4,利用周期性和函数的对称性可以求出f(2010)的值.
解答:解:根据f(x+1)是偶函数可以得出函数f(x)关于x=1对称,又根据f(x)为奇函数,因此该函数是以4为周期的函数,所以f(2010)=f(4×502+2)=f(2)=f(0)=0.
故选:B.
点评:本题考查函数的奇偶性、函数的对称性与函数周期性的关系.解决该类抽象函数的问题一定要弄准函数具备的性质,将所求解的问题进行转化求解.
解答:解:根据f(x+1)是偶函数可以得出函数f(x)关于x=1对称,又根据f(x)为奇函数,因此该函数是以4为周期的函数,所以f(2010)=f(4×502+2)=f(2)=f(0)=0.
故选:B.
点评:本题考查函数的奇偶性、函数的对称性与函数周期性的关系.解决该类抽象函数的问题一定要弄准函数具备的性质,将所求解的问题进行转化求解.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
定义在R上的奇函数f(x)满足f(2x)=-2f(x),f(-1)=
,则f(2)的值为( )
| 1 |
| 2 |
| A、-1 | B、-2 | C、2 | D、1 |