题目内容
定义在R上的奇函数f(x)满足:当x>0时,f(x)=2010x+log2010x,则方程f(x)=0的实根的个数为
3
3
.分析:根据f(x)是R上的奇函数,则f(0)=0,当x>0时,函数f1(x)=2010x,f2(x)=-log2010x的图象有一个交点,方程f(x)=0有唯一实数根,由奇函数的性质知,当x<0时,
也有唯一一个根使得f(x)=0,从而得到结论.
也有唯一一个根使得f(x)=0,从而得到结论.
解答:解:当x>0时,令f(x)=0得,即2010x=-log2010x,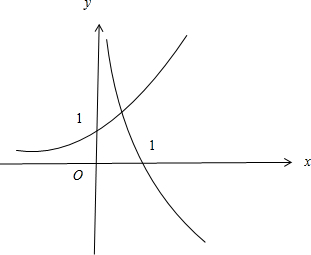
在同一坐标系下分别画出函数f1(x)=2010x,f2(x)=-log2010x的图象,
如右图,可知两个图象只有一个交点,即方程f(x)=0只有一个实根,
∵f(x)是定义在R上的奇函数,
∴当x<0时,方程f(x)=0也有一个实根,
又∵f(0)=0,
∴方程f(x)=0的实根的个数为3.
故答案为 3.

在同一坐标系下分别画出函数f1(x)=2010x,f2(x)=-log2010x的图象,
如右图,可知两个图象只有一个交点,即方程f(x)=0只有一个实根,
∵f(x)是定义在R上的奇函数,
∴当x<0时,方程f(x)=0也有一个实根,
又∵f(0)=0,
∴方程f(x)=0的实根的个数为3.
故答案为 3.
点评:本题主要考查函数的奇偶性,函数的零点与方程的根的关系,体现了转化、数形结合的数学思想,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
定义在R上的奇函数f(x)满足f(2x)=-2f(x),f(-1)=
,则f(2)的值为( )
| 1 |
| 2 |
| A、-1 | B、-2 | C、2 | D、1 |