Question

在坐标平面上，不等式组

y≤2 kx-y≤0 x+ky≥0

（其中k＞0）所表示的平面区域面积的最小值是（　　）

• A．2
• B．4
• C．2

  2

• D．4

  2

Answer 1

分析：先画出不等式组所表示的平面区域，然后表示出图形的面积，最后利用基本不等式求出面积的最值即可．

解答：解：画出不等式组 

y≤2 kx-y≤0 x+ky≥0

所表示的平面区域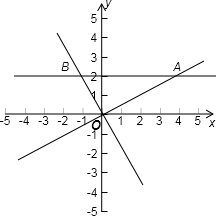
根据题意可知三角形OAB为直角三角形，其面积等于

1

2

×AB×2=AB
点A的坐标为（

2

k

，2），点B的坐标为（-2k，2）
∴S=AB=

2

k

-（-2k）=

2

k

+2k≥4（k＞0）
∴所表示的平面区域面积的最小值是4
故选B

点评：本题考查简单的线性规划，以及利用基本不等式等知识求最值问题，是中档题．