题目内容
【题目】已知向量a=(cos α,sin α),b=(cos β,sin β),c=(-1,0).
(1) 求向量b+c的模的最大值;
(2) 若α=![]() ,且a⊥(b+c),求cos β的值.
,且a⊥(b+c),求cos β的值.
【答案】(1)2(2)见解析
【解析】试题分析(1)根据向量加法坐标表示以及向量模的坐标表示可得|b+c|2=2(1-cos β),再根据三角函数有界性可得模的最值(2)由向量垂直可得数量积为零,根据向量数量积坐标表示可得关于β的方程,解得β值 ,即得cos β的值.
试题解析:解:(1) b+c=(cos β-1,sin β),则|b+c|2=(cos β-1)2+sin2β=2(1-cos β).
∵ -1≤cos β≤1,
∴ 0≤|b+c|2≤4,即0≤|b+c|≤2.
当cos β=-1时,|b+c|取最大值2,
∴ 向量b+c的模的最大值为2.
(2) ∵ b+c=(cos β-1,sin β),
∴ a·(b+c)=cos αcos β-cos α+sin αsin β
=cos(α-β)-cos α.
∵ a⊥(b+c),
∴ a·(b+c)=0,即cos(α-β)=cos α.
又α=![]() ,∴ cos
,∴ cos![]() =cos
=cos![]() ,β-
,β-![]() =2kπ±
=2kπ±![]() (k∈Z),
(k∈Z),
∴ β=2kπ+![]() 或β=2kπ,k∈Z,
或β=2kπ,k∈Z,
∴ cos β=0或cos β=1.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
【题目】某单位每天的用电量![]() (度)与当天最高气温
(度)与当天最高气温![]() (℃)之间具有线性相关关系,下表是该单位随机统计4天的用电量与当天最高气温的数据.
(℃)之间具有线性相关关系,下表是该单位随机统计4天的用电量与当天最高气温的数据.
最高气温(℃) | 26 | 29 | 31 | 34 |
用电量 (度) | 22 | 26 | 34 | 38 |
(Ⅰ)根据表中数据,求出回归直线的方程![]() (其中
(其中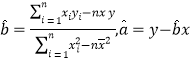 );
);
(Ⅱ)试预测某天最高气温为33℃时,该单位当天的用电量(精确到1度).