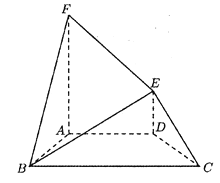
题目内容
【题目】设关于x的一元二次方程x2+ax﹣ ![]() +1=0.
+1=0.
(1)若a是从1,2,3这三个数中任取的一个数,b是从0,1,2这三个数中任取的一个数,求上述方程中有实根的概率;
(2)若a是从区间[0,3]中任取的一个数,b是从区间[0,2]中任取的一个数,求上述方程有实根的概率.
【答案】
(1)解:由题意,知基本事件共有9个,可用有序实数对表示为(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2),
其中第一个表示a的取值,第二个表示b的取值.
由方程 ![]() 的
的 ![]() ,
,
可得,a2+b2≥4,
所以方程 ![]() 有实根包含7个基本事件,
有实根包含7个基本事件,
即(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2).
所以,此时方程 ![]() 有实根的概率为
有实根的概率为 ![]() .
.
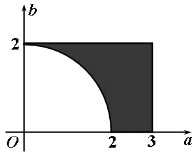
(2)解:a,b的取值所构成的区域如图所示,其中0≤a≤3,0≤b≤2,
∴构成“方程 ![]() 有实根”这一事件的区域为{(a,b)|a2+b2≥4,0≤a≤3,0≤b≤2}(图中阴影部分)
有实根”这一事件的区域为{(a,b)|a2+b2≥4,0≤a≤3,0≤b≤2}(图中阴影部分)
∴此时所求概率为 ![]() .
.
【解析】(1)利用有序实数对表示基本事件,由古典概型公式解答;(2)表示a,b满足的区域,求出面积,利用几何概型解答.

【题目】大学生赵敏利用寒假参加社会实践,对机械销售公司7月份至11月份销售某种机械配件的销售量及销售单价进行了调查,销售单价x元和销售量y件之间的一组数据如表所示:
月份 | 7 | 8 | 9 | 10 | 11 |
销售单价x元 | 9 | 9.5 | 10 | 10.5 | 11 |
销售量y件 | 11 | 10 | 8 | 6 | 5 |
(1)根据7至11月份的数据,求出y关于x的回归直线方程;
(2)预计在今后的销售中,销售量与销售单价仍然服从(1)中的关系,若该种机器配件的成本是2.5元/件,那么该配件的销售单价应定为多少元才能获得最大利润? 参考公式:回归直线方程 ![]() =b
=b ![]() +a,其中b=
+a,其中b= 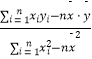 .
.
参考数据: ![]() =392,
=392, ![]() =502.5.
=502.5.
【题目】某公司有一批专业技术人员,对他们进行年龄状况和接受教育程度(学历)的调查,其结果(人数分布)如表:
学历 | 35岁以下 | 35~50岁 | 50岁以上 |
本科 | 80 | 30 | 20 |
研究生 | x | 20 | y |
(Ⅰ)用分层抽样的方法在35~50岁年龄段的专业技术人员中抽取一个容量为10的样本,将该样本看成一个总体,从中任取3人,求至少有1人的学历为研究生的概率;
(Ⅱ)在这个公司的专业技术人员中按年龄状况用分层抽样的方法抽取N个人,其中35岁以下48人,50岁以上10人,再从这N个人中随机抽取出1人,此人的年龄为50岁以上的概率为 ![]() ,求x、y的值.
,求x、y的值.