题目内容
下列命题:
①设函数f(x)=g(x)+x2,曲线y=g(x)在点(1,g(1))处的切线方程为y=2x+1,则曲线y=f(x)在点(1,f(1))处切线的斜率为-
;
②关于x的不等式(a-3)x2<(4a-2)x对任意的a∈(0,1)恒成立,则x的取值范围是(-∞,-1]∪[
,+∞),
③变量X与Y相对应的一组数据为(10,1),(11.3,2),(11.8,3),(12.5,4),(13,5);变量U与V相对应的一组数据为(10,5),(11.3,4),(11.8,3),(12.5,2),(13,1),r1表示变量Y与X之间的线性相关系数,r2表示变量V与U之间的线性相关系数,则r2<0<r1;
④下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据
根据上表提供的数据,得出y关于x的线性回归方程为y=a+0.7x,则a=-0.35;
以上命题正确的个数是( )
①设函数f(x)=g(x)+x2,曲线y=g(x)在点(1,g(1))处的切线方程为y=2x+1,则曲线y=f(x)在点(1,f(1))处切线的斜率为-
| 1 |
| 2 |
②关于x的不等式(a-3)x2<(4a-2)x对任意的a∈(0,1)恒成立,则x的取值范围是(-∞,-1]∪[
| 2 |
| 3 |
③变量X与Y相对应的一组数据为(10,1),(11.3,2),(11.8,3),(12.5,4),(13,5);变量U与V相对应的一组数据为(10,5),(11.3,4),(11.8,3),(12.5,2),(13,1),r1表示变量Y与X之间的线性相关系数,r2表示变量V与U之间的线性相关系数,则r2<0<r1;
④下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
以上命题正确的个数是( )
| A.0 | B.1 | C.2 | D.3 |
①中,f′(x)=g′(x)+2x.
∵y=g(x)在点(1,g(1))处的切线方程为y=2x+1,
∴g′(1)=2,∴f′(1)=g′(1)+2×1=2+2=4,
∴曲线y=f(x)在点(1,f(1))处切线斜率为4,
故①错误.
②中,不等式(a-3)x2<(4a-2)x即(x2-4x)a-3x2+2x<0,
令g(a)=(x2-4x)a-3x2+2x,a∈(0,1)
由题意可得g(a)<0在a∈(0,1)恒成立,结合一次函数的单调性可得
,即
,解不等式组可得x≤-1或x≥
,
∴x的取值范围是(-∞,-1]∪[
,+∞),
故②正确;
③中,∵变量X与Y相对应的一组数据为(10,1),(11.3,2),(11.8,3),(12.5,4),(13,5),
=
11.72,
=
=3,
∴这组数据的相关系数是r=
=0.3755,
变量U与V相对应的一组数据为(10,5),(11.3,4),(11.8,3),(12.5,2),(13,1)
=
=3,
∴这组数据的相关系数是-0.3755,
∴第一组数据的相关系数大于零,第二组数据的相关系数小于零,即r2<0<r1,
故③正确;
④中,由对照数据,计算得
xi2=86,
=
=4.5,
=
=3.5,
xiyi=66.5,4
=63,4
2=81,
∴求得回归方程的系数为b=0.7,a=0.35,
∴所求线性回归方程为y=0.7x+0.35,
故④错误;
故选C.
∵y=g(x)在点(1,g(1))处的切线方程为y=2x+1,
∴g′(1)=2,∴f′(1)=g′(1)+2×1=2+2=4,
∴曲线y=f(x)在点(1,f(1))处切线斜率为4,
故①错误.
②中,不等式(a-3)x2<(4a-2)x即(x2-4x)a-3x2+2x<0,
令g(a)=(x2-4x)a-3x2+2x,a∈(0,1)
由题意可得g(a)<0在a∈(0,1)恒成立,结合一次函数的单调性可得
|
|
| 2 |
| 3 |
∴x的取值范围是(-∞,-1]∪[
| 2 |
| 3 |
故②正确;
③中,∵变量X与Y相对应的一组数据为(10,1),(11.3,2),(11.8,3),(12.5,4),(13,5),
| . |
| X |
| 10+11.3+11.8+12.5+13.5 |
| 5 |
| . |
| Y |
| 1+2+3+4+5 |
| 5 |
∴这组数据的相关系数是r=
| 7.2 |
| 19.172 |
变量U与V相对应的一组数据为(10,5),(11.3,4),(11.8,3),(12.5,2),(13,1)
| . |
| V |
| 5+4+3+2+1 |
| 5 |
∴这组数据的相关系数是-0.3755,
∴第一组数据的相关系数大于零,第二组数据的相关系数小于零,即r2<0<r1,
故③正确;
④中,由对照数据,计算得
| 4 |
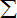 |
| i=1 |
| . |
| x |
| 3+4+5+6 |
| 4 |
| . |
| y |
| 2.5+3+4+4.5 |
| 4 |
| 4 |
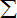 |
| i=1 |
| . |
| x |
| . |
| •y |
| . |
| x |
∴求得回归方程的系数为b=0.7,a=0.35,
∴所求线性回归方程为y=0.7x+0.35,
故④错误;
故选C.

练习册系列答案
相关题目