题目内容
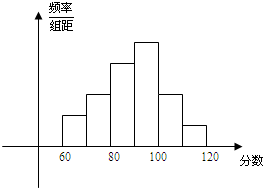为了了解高二学生的数学成绩，抽取了某班60名学生，将所得数据整理后，画出其频率分布直方图（如图），已知从左到右各长方形高的比为2：3：5：6：3：1，则该班学生数学成绩在（80，100）之间的学生人数是（ ）| A、32人 | B、27人 | C、24人 | D、33人 |
分析：根据题意可得该班六个分数段的概率比例依次为2：3：5：6：3：1，进而得到成绩在（80，90）与（90，100）之间的学生人数的概率，即可得到答案．
解答：解：由题意可得：从左到右各长方形高的比为2：3：5：6：3：1，
所以（60，70），（70，80），（80，90），（90，100），（100，110），（110，120）各分数段的概率之比为2：3：5：6：3：1，
所以该班学生数学成绩在（80，90）与（90，100）之间的学生人数的概率分别为：
，
．
所以该班学生数学成绩在（80，100）之间的学生人数是：60×(
+
)=33．
故选D．
所以（60，70），（70，80），（80，90），（90，100），（100，110），（110，120）各分数段的概率之比为2：3：5：6：3：1，
所以该班学生数学成绩在（80，90）与（90，100）之间的学生人数的概率分别为：
| 1 |
| 4 |
| 3 |
| 10 |
所以该班学生数学成绩在（80，100）之间的学生人数是：60×(
| 1 |
| 4 |
| 3 |
| 10 |
故选D．
点评：解决此类问题的关键是熟练掌握频率分布直方图的中长方形的高与事件发生的概率之间的关系．
练习册系列答案
相关题目
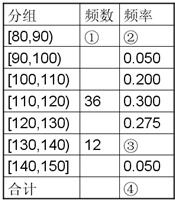
某校高二年级有500名学生，为了了解数学学科的学习情况，现从中随机抽出若干名学生在一次测试中的数学成绩，制成如下频率分布表：| 分组 | 频数 | 频率 |
| [85，95） | ① | ② |
| [95，105） | 0.050 | |
| [105，115） | 0.200 | |
| [115，125） | 12 | 0.300 |
| [125，135） | 0.275 | |
| [135，145） | 4 | ③ |
| [145，155] | 0.050 | |
| 合计 | ④ |
（2）在所给的坐标系中画出区间[85，155]上的频率分布直方图；
（3）假定125分及其以上为优秀，根据抽样结果估计高二年级这次数学测试的优秀人数．
青少年的视力水平的下降已经引起全社会的关注，某校为了了解高二年级500名学生的视力情况，从中抽查一部分学生视力，通过数据处理，得到如下频率分布表．可是粗心的调查员却把表中的五个数据抄丢了．（本小题满分12分）某校高二年级有500名学生，为了了解数学学科的学习情况，现从中随机抽出若干名学生在一次测试中的数学成绩，制成如下频率分布表：
| 分组 | 频数 | 频率 |
| [85,95) | ① | ② |
| [95,105) | | 0.050 |
| [105,115) | | 0.200 |
| [115,125) | 12 | 0.300 |
| [125,135) | | 0.275 |
| [135,145) | 4 | ③ |
| [145,155) | | 0.050 |
| 合计 | | ④ |
(1)根据上面图表，①②③④处的数值分别为________、________、________、________；
(2)在所给的坐标系中画出[85,155]的频率分布直方图；
(3)根据题中信息估计总体平均数，并估计总体落在[129,155]中的频率．
