题目内容
 某校高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
某校高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:| 分组 | 频数 | 频率 |
| [85,95) | ① | ② |
| [95,105) | 0.050 | |
| [105,115) | 0.200 | |
| [115,125) | 12 | 0.300 |
| [125,135) | 0.275 | |
| [135,145) | 4 | ③ |
| [145,155] | 0.050 | |
| 合计 | ④ |
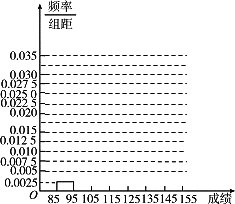
(2)在所给的坐标系中画出区间[85,155]上的频率分布直方图;
(3)假定125分及其以上为优秀,根据抽样结果估计高二年级这次数学测试的优秀人数.
分析:(1)由数学成绩落在区间[115,125)的频数为12,频率为0.300,我们易求出样本容量,进而确定①②③④处的数值
(2)根据(1)中所得的各组数据的频率,我们可计算出各组数据对应矩形的高,进而画出满足条件的频率分布直方图;
(3)根据(1)中所得的各组数据的频率,我们可计算出125分及其以上的频率,然后根据总体容量为500,估计出这次考试高二年级这次数学测试的优秀人数.
(2)根据(1)中所得的各组数据的频率,我们可计算出各组数据对应矩形的高,进而画出满足条件的频率分布直方图;
(3)根据(1)中所得的各组数据的频率,我们可计算出125分及其以上的频率,然后根据总体容量为500,估计出这次考试高二年级这次数学测试的优秀人数.
解答:解:(1)∵数学成绩落在区间[115,125)的频数为12,频率为0.300,
∴参与抽查的样本容量为
=40
由于合计的频率和一定为1,故④应填1;
由数学成绩落在区间[135,145)的频数为4,可得其频率为
=0.100,故③应填0.100;
由于各组频率和为1,故②应填0.025,①应填1;
故答案为:1,0.025,0.100,1;
(2)区间[85,155]上的频率分布直方图如下图所示:
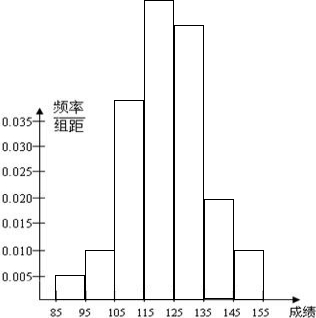
(3)由(1)可知,分数在125分以上的频率和为0.275+0.100+0.050=0.425
则高二年级这次数学测试的优秀人数约为500×0.425=212.5人
∴参与抽查的样本容量为
| 12 |
| 0.300 |
由于合计的频率和一定为1,故④应填1;
由数学成绩落在区间[135,145)的频数为4,可得其频率为
| 4 |
| 40 |
由于各组频率和为1,故②应填0.025,①应填1;
故答案为:1,0.025,0.100,1;
(2)区间[85,155]上的频率分布直方图如下图所示:

(3)由(1)可知,分数在125分以上的频率和为0.275+0.100+0.050=0.425
则高二年级这次数学测试的优秀人数约为500×0.425=212.5人
点评:本题考查的知识点是频率分布直方图,用样本的频率分布估计总体分布,其中频率=
=矩形高×组距是解答此类问题的关键.
| 频数 |
| 样本容量 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(本小题满分12分)某校高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
| 分组 | 频数 | 频率 |
| [85,95) | ① | ② |
| [95,105) | | 0.050 |
| [105,115) | | 0.200 |
| [115,125) | 12 | 0.300 |
| [125,135) | | 0.275 |
| [135,145) | 4 | ③ |
| [145,155) | | 0.050 |
| 合计 | | ④ |

(1)根据上面图表,①②③④处的数值分别为________、________、________、________;
(2)在所给的坐标系中画出[85,155]的频率分布直方图;
(3)根据题中信息估计总体平均数,并估计总体落在[129,155]中的频率.
 某校高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
某校高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
| 分组 | 频数 | 频率 |
| [85,95) | ① | ② |
| [95,105) | 0.050 | |
| [105,115) | 0.200 | |
| [115,125) | 12 | 0.300 |
| [125,135) | 0.275 | |
| [135,145) | 4 | ③ |
| [145,155] | 0.050 | |
| 合计 | ④ |
(2)在所给的坐标系中画出区间[85,155]上的频率分布直方图;
(3)假定125分及其以上为优秀,根据抽样结果估计高二年级这次数学测试的优秀人数.