题目内容
17.设函数f(x)=1-|2x-3|,g(x)=$\sqrt{x}$-$\sqrt{x-a}$.(1)求不等式f(x)≥3x+1的解集;
(2)若0<a<b,M=g(a+b),N=g(b),求证:M<N.
分析 (1)通过讨论x的范围,解不等式,从而求出不等式的解集;(2)分别表示出M,N,结合a,b的范围通过比较分母从而比较出M、N的大小.
解答 解:(1)∵f(x)=1-|2x-3|,
∴1-|2x-3|≥3x+1,即|2x-3|≤-3x,
①x≤$\frac{3}{2}$时,-(2x-3)≤-3x,解得:x≤-3;
②x>$\frac{3}{2}$时,(2x-3)≤-3x,解得:x<$\frac{3}{5}$,舍,
故不等式f(x)≥3x+1的解集是:{x|x≤-3};
(2)M=g(a+b)=$\sqrt{a+b}$-$\sqrt{b}$=$\frac{a}{\sqrt{a+b}+\sqrt{b}}$,
N=g(b)=$\sqrt{b}$-$\sqrt{b-a}$=$\frac{a}{\sqrt{b}+\sqrt{b-a}}$,
比较分母,易得:$\sqrt{a+b}$>$\sqrt{b-a}$,
∴M<N.
点评 本题考查了解绝对值不等式问题,考查比较大小的方法,本题属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.△ABC中,角A,B,C的对边分别为a,b,c,B=2A,a=1,b=$\frac{4}{3}$,则△ABC一定是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 不能确定 |
12.设集合M={0,1,2,3},N={x|x2-3x+2≤0},则M∩N=( )
| A. | {0} | B. | {1} | C. | {0,1} | D. | {1,2} |
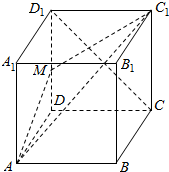 如图M是棱长为2的正方体ABCD-A1B1C1D1的棱DD1的中点.
如图M是棱长为2的正方体ABCD-A1B1C1D1的棱DD1的中点.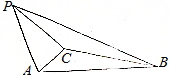 如图,在三棱锥P-ABC中,PA⊥平面ABC,∠ACB=90°,∠BAC=60°,PA=AC=1.
如图,在三棱锥P-ABC中,PA⊥平面ABC,∠ACB=90°,∠BAC=60°,PA=AC=1. 如图,AB是圆O的直径,点C在圆O上,矩形DCBE所在的平面垂直于圆O所在的平面,AB=4,BE=1.
如图,AB是圆O的直径,点C在圆O上,矩形DCBE所在的平面垂直于圆O所在的平面,AB=4,BE=1.