题目内容

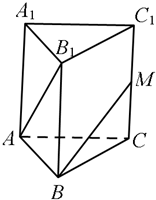如图，已知三棱柱ABC-A1B1C1的各条棱长都相等，且CC1⊥底面ABC，M是侧棱CC1的中点，则异面直线AB1和BM所成的角的大小是（　　）
分析：由题意设棱长为a，补正三棱柱ABC-A2B2C2，构造直角三角形A2BM，解直角三角形求出BM，利用勾股定理求出A2M，从而求解．
解答：解：设棱长为a，补正三棱柱ABC-A2B2C2（如图）．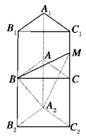
平移AB1至A2B，连接A2M，∠MBA2即为AB1与BM所成的角，
在△A2BM中，A2B=
2
a，BM=
a2+(
a
2
)2
=
5
2
a，
A2M=
a2+(
3a
2
)2
=
13
2
a，
∴A2B2+BM2=A2M2，
∴∠MBA2=
π
2
．
故选D
点评：此题主要考查了异面直线及其所成的角和勾股定理的应用，计算比较复杂，要仔细的做．
练习册系列答案
相关题目
精英家教网如图，已知三棱柱ABC-A1B1C1中，AA1⊥底面ABC，AC=BC=2，AA1=4，AB=2
2
，M，N分别是棱CC1，AB中点．
（Ⅰ）求证：CN⊥平面ABB1A1；
（Ⅱ）求证：CN∥平面AMB1；
（Ⅲ）求三棱锥B1-AMN的体积．
精英家教网如图，已知三棱柱ABC-A1B1C1的侧棱与底面垂直，AA1=AB=AC=1，且AB⊥AC，M是CC1的中点，N是BC的中点，点P在直线A1B1上，且满足
A1P
=λ
A1B1
．
（1）证明：PN⊥AM；
（2）当λ取何值时，直线PN与平面ABC所成的角θ最大？并求该角最大值的正切值．
如图，已知三棱柱ABC-A1B1C1的侧棱与底面垂直，AA1=AB=AC=1，AB⊥AC，M，N分别是CC1，BC的中点，点P在直线A1B1上，且
A1P
=λ
A1B1
；
（Ⅰ）证明：无论λ取何值，总有AM⊥PN；
（Ⅱ）当λ取何值时，直线PN与平面ABC所成的角θ最大？并求该角取最大值时的正切值；
（Ⅲ）是否存在点P，使得平面PMN与平面ABC所成的二面角为30°，若存在，试确定点P的位置，若不存在，请说明理由．
如图，已知三棱柱ABC-A1B1C1的所有棱长均为2，且A1A⊥底面ABC，D为AB的中点，G为△ABC1的重心，则|
CG
|的值为（　　）
精英家教网如图，已知三棱柱ABC-A1B1C1中，AA1⊥平面ABC，AB=BC，∠ABC=90°，D为AC中点．
（1）求证：BD⊥AC1；
（2）若AB=
2
，AA1=2
3
，求AC1与平面ABC所成的角．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网