题目内容
已知x,y,z∈R,且x+y+z=1,x2+y2+z2= ,
,
证明:x,y,z∈[0, ]
]
 ,
,证明:x,y,z∈[0,
 ]
]证明略
证法一: 由x+y+z=1,x2+y2+z2= ,得x2+y2+(1-x-y)2=
,得x2+y2+(1-x-y)2= ,整理成关于y的一元二次方程得:
,整理成关于y的一元二次方程得:
2y2-2(1-x)y+2x2-2x+ =0,∵y∈R,故Δ≥0
=0,∵y∈R,故Δ≥0
∴4(1-x)2-4×2(2x2-2x+ )≥0,得0≤x≤
)≥0,得0≤x≤ ,∴x∈[0,
,∴x∈[0, ]
]
同理可得y,z∈[0, ]
]
证法二: 设x= +x′,y=
+x′,y= +y′,z=
+y′,z= +z′,则x′+y′+z′=0,
+z′,则x′+y′+z′=0,
于是 =(
=( +x′)2+(
+x′)2+( +y′)2+(
+y′)2+( +z′)2
+z′)2
= +x′2+y′2+z′2+
+x′2+y′2+z′2+ (x′+y′+z′)
(x′+y′+z′)
= +x′2+y′2+z′2≥
+x′2+y′2+z′2≥ +x′2+
+x′2+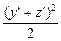 =
= +
+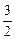 x′2
x′2
故x′2≤ ,x′∈[-
,x′∈[- ,
, ],x∈[0,
],x∈[0, ],同理y,z∈[0,
],同理y,z∈[0, ]
]
证法三: 设x、y、z三数中若有负数,不妨设x<0,则x2>0,
 =x2+y2+z2≥x2+
=x2+y2+z2≥x2+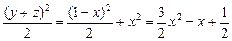 >
> ,矛盾
,矛盾
x、y、z三数中若有最大者大于 ,不妨设x>
,不妨设x> ,
,
则 =x2+y2+z2≥x2+
=x2+y2+z2≥x2+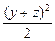 =x2+
=x2+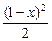 =
=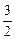 x2-x+
x2-x+
=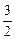 x(x-
x(x- )+
)+ >
>
 矛盾
矛盾
故x、y、z∈[0, ]
]
 ,得x2+y2+(1-x-y)2=
,得x2+y2+(1-x-y)2= ,整理成关于y的一元二次方程得:
,整理成关于y的一元二次方程得: 2y2-2(1-x)y+2x2-2x+
 =0,∵y∈R,故Δ≥0
=0,∵y∈R,故Δ≥0∴4(1-x)2-4×2(2x2-2x+
 )≥0,得0≤x≤
)≥0,得0≤x≤ ,∴x∈[0,
,∴x∈[0, ]
]同理可得y,z∈[0,
 ]
]证法二: 设x=
 +x′,y=
+x′,y= +y′,z=
+y′,z= +z′,则x′+y′+z′=0,
+z′,则x′+y′+z′=0,于是
 =(
=( +x′)2+(
+x′)2+( +y′)2+(
+y′)2+( +z′)2
+z′)2=
 +x′2+y′2+z′2+
+x′2+y′2+z′2+ (x′+y′+z′)
(x′+y′+z′)=
 +x′2+y′2+z′2≥
+x′2+y′2+z′2≥ +x′2+
+x′2+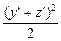 =
= +
+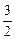 x′2
x′2故x′2≤
 ,x′∈[-
,x′∈[- ,
, ],x∈[0,
],x∈[0, ],同理y,z∈[0,
],同理y,z∈[0, ]
]证法三: 设x、y、z三数中若有负数,不妨设x<0,则x2>0,
 =x2+y2+z2≥x2+
=x2+y2+z2≥x2+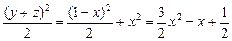 >
> ,矛盾
,矛盾
x、y、z三数中若有最大者大于
 ,不妨设x>
,不妨设x> ,
,则
 =x2+y2+z2≥x2+
=x2+y2+z2≥x2+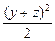 =x2+
=x2+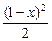 =
=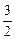 x2-x+
x2-x+
=
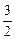 x(x-
x(x- )+
)+ >
>
 矛盾
矛盾
故x、y、z∈[0,
 ]
]
练习册系列答案
相关题目
 ,证明:
,证明: .
.




 个等式,并猜测第
个等式,并猜测第 (
(
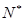 )个等式;
)个等式;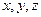 均为正数,
均为正数, ,则
,则 的最小值是 ( )
的最小值是 ( )



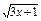 +
+ +
+ ≤3
≤3 ;
; 是定义在正整数集上的函数,且
是定义在正整数集上的函数,且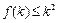 成立时,总可推出
成立时,总可推出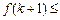
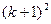 成立”.那么,下列命题总成立的是
成立”.那么,下列命题总成立的是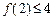 成立,则当
成立,则当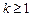 时,均有
时,均有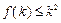 成立
成立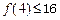 成立,则当
成立,则当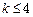 时,均有
时,均有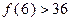 成立,则当
成立,则当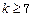 时,均有
时,均有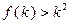 成立
成立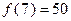 成立,则当
成立,则当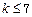 时,均有
时,均有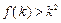 成立
成立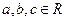 ,求证:
,求证: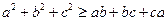 .
.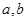 使得
使得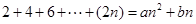 对一切
对一切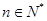 恒成立?若存在,求出
恒成立?若存在,求出 、
、 、
、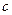 为实数,
为实数, ,则下列四个结论中正确的是( )
,则下列四个结论中正确的是( )


