题目内容
知x、y、z均为实数,
(1)若x+y+z=1,求证: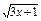 +
+ +
+ ≤3
≤3 ;
;
(2)若x+2y+3z=6,求x2+y2+z2的最小值.
(1)若x+y+z=1,求证:
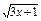 +
+ +
+ ≤3
≤3 ;
;(2)若x+2y+3z=6,求x2+y2+z2的最小值.
(1)证明略(2)x2+y2+z2的最小值为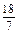
(1)证明 因为(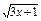 +
+ +
+ )2
)2
≤(12+12+12)(3x+1+3y+2+3z+3)=27.
所以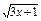 +
+ +
+ ≤3
≤3 . 7分
. 7分
(2)解 因为(12+22+32)(x2+y2+z2)
≥(x+2y+3z)2=36,
即14(x2+y2+z2)≥36,
所以x2+y2+z2的最小值为 . 14分
. 14分
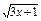 +
+ +
+ )2
)2≤(12+12+12)(3x+1+3y+2+3z+3)=27.
所以
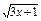 +
+ +
+ ≤3
≤3 . 7分
. 7分(2)解 因为(12+22+32)(x2+y2+z2)
≥(x+2y+3z)2=36,
即14(x2+y2+z2)≥36,
所以x2+y2+z2的最小值为
 . 14分
. 14分 
练习册系列答案
相关题目
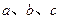 均为正实数,满足关系式
均为正实数,满足关系式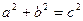 ,又
,又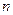 为不小于
为不小于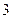 的自然数,求证:
的自然数,求证: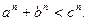
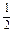 ;
;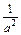 +
+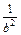 ≥8;
≥8;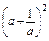 +
+ 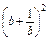 ≥
≥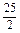 ;
;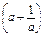
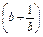 ≥
≥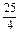 .
.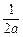 +
+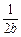 +
+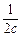 ≥
≥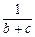 +
+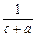 +
+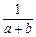 .
.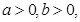 那么
那么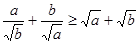 。
。 ,
, ]
]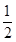 +
+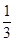 +
+ 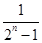 <f(n) (n≥2,
<f(n) (n≥2,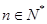 )的过程中,由n=k变到n=k+1时,左边增加了( )
)的过程中,由n=k变到n=k+1时,左边增加了( )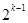 项
项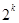 项
项 、
、 ,求证:
,求证: .
.