Question

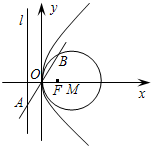已知抛物线C：y²=2px（p＞0）的准线为l，焦点为F．⊙M的圆心在x轴的正半轴上，且与y轴相切．过原点O作倾斜角为

π

3

的直线n，交l于点A，交⊙M于另一点B，且AO=OB=2．
（Ⅰ）求⊙M和抛物线C的方程；
（Ⅱ）若P为抛物线C上的动点，求

PM

•

PF

的最小值；
（Ⅲ）过l上的动点Q向⊙M作切线，切点为S，T，求证：直线ST恒过一个定点，并求该定点的坐标．

Answer 1

分析：（I）根据

p

2

=1=OA•cos60°可求出p的值，从而求出抛物线方程，求出圆心和半径可求出⊙M的方程；
（II）先表示出

PM

•

PF

然后根据点在抛物线上将y消去，求关于x 的二次函数的最小值即可；
（III）以点Q这圆心，QS为半径作⊙Q，则线段ST即为⊙Q与⊙M的公共弦，设点Q（-1，t），根据QS²=QM²-4=t²+5，求出直线ST的方程，使直线与t无关，可求出定点坐标．

解答：解：（Ⅰ）因为

p

2

=OA•cos60°=2×

1

2

=1，即p=2，所以抛物线C的方程为y²=4x（2分）
设⊙M的半径为r，则r=

OB

2

•

1

cos60°

=2，所以⊙M的方程为（x-2）²+y²=4（5分）
（Ⅱ）设P（x，y）（x≥0），则

PM

•

PF

=(2-x，-y)(1-x，-y)=x²-3x+2+y²=x²+x+2（8分）
所以当x=0时，

PM

•

PF

有最小值为2（10分）
（Ⅲ）以点Q这圆心，QS为半径作⊙Q，则线段ST即为⊙Q与⊙M的公共弦（11分）
设点Q（-1，t），则QS²=QM²-4=t²+5，
所以⊙Q的方程为（x+1）²+（y-t）²=t²+5（13分）
从而直线ST的方程为3x-ty-2=0（*）（14分）
因为

x= 2 3 y=0

一定是方程（*）的解，所以直线ST恒过一个定点，且该定点坐标为(

2

3

，0)（16分）

点评：本题主要考查了圆的方程和抛物线方程，以及向量数量积的最值和直线恒过定点问题，是一道综合题，有一定的难度．