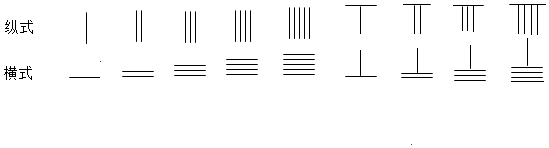
题目内容
【题目】四支足球队进行单循环比赛（每两队比赛一场），每场比赛胜者得3分，负者得0分，平局双方各得1分．比赛结束后发现没有足球队全胜，且四队得分各不相同，则所有比赛中最多可能出现的平局场数是（ ）
A.2
B.3
C.4
D.5
【答案】C
【解析】解：四支足球队进行单循环比赛（每两队比赛一场），共比赛6场．
每场比赛胜者得3分，负者得0分，平局双方各得1分．即每场比赛若不平局，则共产生3×6=18分，每场比赛都平局，则共产生2×6=12分．
比赛结束后发现没有足球队全胜，且四队得分各不相同，则各队得分分别为：2，3，4，5；或3，4，5，6．
如果是3，4，5，6，则每场产生 
=3分，没有平局产生，但是不可能产生4，5分，与题意矛盾，舍去．
因此各队得分分别为：2，3，4，5．第一名得分5：5=3+1+1，为一胜两平；第二名得分4：4=3+1+0，为一胜一平一负；第三名得分3：根据胜场等于负场，只能为三平；第四名得分2：2=1+1+0，为两平一负．则所有比赛中最多可能出现的平局场数是4．
故答案选：C．
本题考查的是排列组合的问题。
【题目】某种产品的质量以其质量指标衡量，并依据质量指标值划分等级如表：
质量指标值m | m＜185 | 185≤m＜205 | M≥205 |
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件，检测后得到如下的频率分布直方图：
（1）根据以上抽样调查的数据，能否认为该企业生产这种产品符合“一、二等品至少要占到全部产品的92%的规定”？
（2）在样本中，按产品等级用分层抽样的方法抽取8件，再从这8件产品中随机抽取4件，求抽取的4件产品中，一、二、三等品都有的概率；
（3）该企业为提高产品的质量，开展了“质量提升月”活动，活动后再抽样检测，产品质量指标值X近似满足X～N（218，140），则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少？
