题目内容
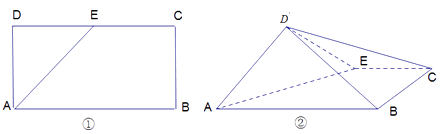
【题目】如图①，在矩形 
中， 
， 
是 
的中点，将三角形 
沿 
翻折到图②的位置，使得平面 
平面 
.
（1）在线段 
上确定点 
，使得 
平面 
，并证明；
（2）求 
与 
所在平面构成的锐二面角的正切值.
【答案】
（1）解：点 
是线段 
中点时， 
平面 
.
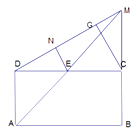
证明：记 
， 
的延长线交于点 
，因为 
，所以点 
是 
的中点，所以 
.
而 
在平面 内， 
在平面 外，所以 平面 .
（2）解：在矩形 
中， 
， 
，
因为平面 
平面 
，且交线是 ，所以 平面 .
在平面 内作 
，连接 
，则 .
所以 
就是 
与 
所在平面构成的锐二面角的平面角.
因为 
, 
，所以 
.
【解析】(1)注意平面图形的翻折时,在一个面内的因素是不变化的,涉及到两个面的因素才可能变化,先找到中点,使得直线与平面图平行;
(2)找到二面角的一个平面角,通过解三角形求角.
练习册系列答案
相关题目
【题目】某企业生产A，B两种产品，生产每一吨产品所需的劳动力、煤和电如下表：
产品品种 | 劳动力(个) | 煤(吨) | 电(千瓦时) |
A产品 | 3 | 9 | 4 |
B产品 | 10 | 4 | 5 |
已知生产每吨A产品的利润是7万元，生产每吨B产品的利润是12万元，现因条件限制，该企业仅有劳动力300个，煤360吨，并且供电局只能供电200千瓦时，试问该企业如何安排生产，才能获得最大利润？
