题目内容
 (本小题满分18分)如图,将圆分成
(本小题满分18分)如图,将圆分成![]() 个扇形区域,用3种不同颜色给每一个扇形区域染色,要求相邻区域颜色互异,把不同的染色方法种数记为
个扇形区域,用3种不同颜色给每一个扇形区域染色,要求相邻区域颜色互异,把不同的染色方法种数记为![]() 。求
。求
(Ⅰ)![]() ;
;
(Ⅱ)![]() 与
与![]() 的关系式;
的关系式;
(Ⅲ)数列![]() 的通项公式
的通项公式![]() ,并证明
,并证明![]() 。
。
解析:(Ⅰ) 当![]() 时,不同的染色方法种数
时,不同的染色方法种数![]() ,……………………1分
,……………………1分
当![]() 时,不同的染色方法种数
时,不同的染色方法种数![]() ,……………………………2分
,……………………………2分
当![]() 时,不同的染色方法种数
时,不同的染色方法种数![]() ,……………………………3分
,……………………………3分
当![]() 时,分扇形区域1,3同色与异色两种情形
时,分扇形区域1,3同色与异色两种情形
∴不同的染色方法种数![]() 。…………………4分
。…………………4分
(Ⅱ)依次对扇形区域![]() 染色,不同的染色方法种数为
染色,不同的染色方法种数为![]() ,其中扇形区域1与
,其中扇形区域1与![]() 不同色的有
不同色的有![]() 种,扇形区域1与
种,扇形区域1与![]() 同色的有
同色的有![]() 种
种
∴![]() …………………………………………………8分
…………………………………………………8分
(Ⅲ)∵![]()
∴![]()
![]()
………………
![]()
将上述![]() 个等式两边分别乘以
个等式两边分别乘以![]() ,再相加,得
,再相加,得
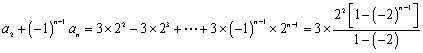 ,
,
∴![]() ,…………………………………………………13分
,…………………………………………………13分
从而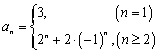 。………………………………………14分
。………………………………………14分
(Ⅲ)证明:当![]() 时,
时,![]()
当![]() 时,
时,![]() ,
,
当![]() 时,
时,
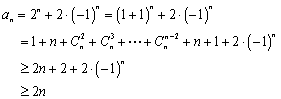 ,
,

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
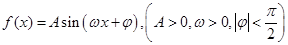 的图象的一部分如下图所示。
的图象的一部分如下图所示。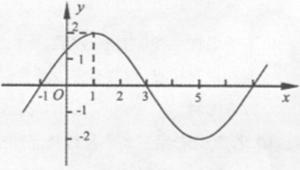
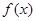 的解析式;
的解析式;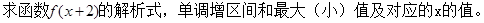
 中,
中,
 项和
项和 ;
; 项和为
项和为 ,若
,若 对任意
对任意 恒成立,求
恒成立,求 的最小值.
的最小值. 是定义域为R的奇函数.
是定义域为R的奇函数. 时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集; 恒成立的
恒成立的 的取值范围;
的取值范围;