��Ŀ����
(��С������18��)��֪���У�an������bn������cn����ͨ�ʽ����bn=an+1-an��cn=bn+1-bn��n��N*?���������У�bn����һ�����㳣���У�������У�an����һ�Ȳ����У������У�cn����һ�����㳣���У�������У�an���Ƕ��Ȳ�����?(1)��д����������a������,b1=1��cn=1��n��N*?���Ķ��Ȳ����У�an����ǰ���(2)����������(1)�Ķ��Ȳ����У�an����ͨ�ʽan��(3)�����У�an������a��������������cn-bn+1+3an��-2n+1��n��N*?���������У�an����ͨ�ʽ
��1��a1=1��a2=2��a3=4��a4=7��a5=11��2��an��(n2-n+2)/2 ��3��an=4n-2n
����:
��1��a1=1��a2=2��a3=4��a4=7��a5=11-----4��
��2��������bn+1-bn=cn=1��n=1��2��3����
����bn=��bn-bn-1������bn-1-bn-2������bn-2-bn-3������+��b2-b1��+b1=1+1+1+��+1=n ---6��
��an+1-an=bn��n��n=1��2��3��������an����an-an-1������an-1-an-2������an-2-an-3������+��a2-a1����a��
=��n-1��+��n-2��+��+2+1+1=n��n-1��/2+1=(n2-n+2)/2 --10��
��3������֪cn-bn+1����an= -2n+1���ɵ�bn+1-bn-bn+1+3an��-2n+1����bn-3an=2n+1����an+1=4an+2n+1�� -12��
�ⷨһ�������ã�an+1����n+1=4��an+2n����-------15��
������У�an+2n��������Ϊa1+2=4������Ϊ4�ĵȱ����У�
��an+2n��4��4n-1����n����an=4n-2n����18�֣�
�ⷨ�����ڵ�ʽan+1��4an+2n+1����ͬʱ����2n+1�ã�an+1/��n+1=2��an/2n������----15��
��kn=an/2n����kn+1����kn+1����kn+1����������kn+1��
�����У�kn+1��������Ϊ2������Ϊ2�ĵȱ���������kn+1=2��2n-1����n����kn=2n-1��
��an=2nkn=2n����n-1��=4n-2n�� -------18��
�ⷨ������a����������a2����������������2��-1����a3��������������������-1����a4��������������������-1��
���룺an=2n��2n-1������n-2n�� ------15��
��������ѧ���ɷ�֤�����£���i����n=1ʱ��a��������4-2�����������
��ii������n=kʱ�������������ak=4k-2k����ô��n=k+1ʱ��ak+1����ak+2k+1������4k-2k������k+1=4 k+1-2 k+1������Ҳ�������ɣ�i������ii����֪��an=4n-2n��----18��

 ���������ʱ��ѵϵ�д�
���������ʱ��ѵϵ�д� �㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
�㽭�¿γ���άĿ�������ʱ��ѵϵ�д� ��������ϵ�д�
��������ϵ�д� ���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д� ����С������18�֣���ͼ����Բ�ֳ�
����С������18�֣���ͼ����Բ�ֳ�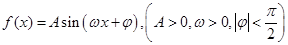 ��ͼ���һ��������ͼ��ʾ��
��ͼ���һ��������ͼ��ʾ��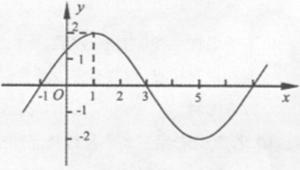
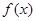 �Ľ���ʽ��
�Ľ���ʽ��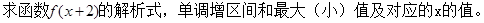
 �У�
�У�
 ���
��� ��
�� ���Ϊ
���Ϊ ����
���� ������
������ ���������
��������� ����Сֵ.
����Сֵ. �Ƕ�����ΪR���溯����
�Ƕ�����ΪR���溯���� ʱ�����жϺ��������Բ���ʽf(x2��2x)��f(x��4)>0�Ľ⼯��
ʱ�����жϺ��������Բ���ʽf(x2��2x)��f(x��4)>0�Ľ⼯�� �������
������� ��ȡֵ��Χ��
��ȡֵ��Χ��