题目内容
3.在正方体ABCD-A1B1C1D1中,二面角A1-BD-A的余弦值大小是$\frac{\sqrt{3}}{3}$.分析 取BD的中点O,连接OA1,OA,则∠AOA1就是二面角A1-BD-A的平面角,由此能求出二面角A1-BD-A的余弦值.
解答 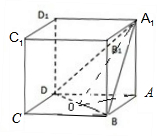 解:设正方体ABCD-A1B1C1D1的棱长为a,
解:设正方体ABCD-A1B1C1D1的棱长为a,
则BD=A1D=A1B=$\sqrt{2}$a,AD=BA=AA1=a,
取BD的中点O,连接OA1,OA,则∠AOA1就是二面角A1-BD-A的平面角,
∵AO=$\frac{1}{2}$BD=$\frac{\sqrt{2}}{2}$a,A10=$\sqrt{{a}^{2}+({\frac{\sqrt{2}}{2}a)}^{2}}$=$\frac{\sqrt{6}a}{2}$
∴cos∠AOA1=$\frac{\frac{\sqrt{2}}{2}a}{\frac{\sqrt{6}a}{2}}$=$\frac{\sqrt{3}}{3}$.
故答案为:$\frac{\sqrt{3}}{3}$.
点评 本题考查二面角的余弦值的求法,是中档题.解题时要认真审题,正方体性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.设a=sin393°,b=cos55°,c=tan50°,则a,b,c的大小关系为( )
| A. | a<b<c | B. | c<b<a | C. | b<a<c | D. | a<c<b |
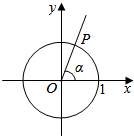 直角坐标系xOy中,锐角α的终边与单位圆的交点为P,将OP绕O逆时针旋转到OQ,使∠POQ=α,其中Q是OQ与单位圆的交点,设Q的坐标为(x,y).
直角坐标系xOy中,锐角α的终边与单位圆的交点为P,将OP绕O逆时针旋转到OQ,使∠POQ=α,其中Q是OQ与单位圆的交点,设Q的坐标为(x,y).