题目内容
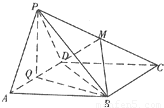
 如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.
如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.(1)求点P到平面ABCD的距离;
(2)求证:PA∥平面MBD;
(3)试问:在线段AB上是否存在一点N,使得平面PCN⊥平面PQB?若存在,试指出点N的位置,并证明你的结论;若不存在,请说明理由.
分析:(1)由已知中,Q为AD的中点,△PAD为正三角形,易得PQ⊥AD,又由ABCD所在平面与正△PAD所在平面互相垂直,由面面垂直的性质,可得PQ即为P到平面ABCD的距离,解三角形PAD即可得到答案.
(2)连AC交BD于O,连MO,由三角形的中位线定理,可得PA∥OM,结合线面平行的判定定理,即可得到PA∥平面MBD;
(3)令N为AB中点,结合(1)中结论易得PQ⊥CN,又由正方形ABCD中Q,N分别为AD,AB中点,则CN⊥BQ,结合线面垂直的判定定理,可得CN⊥平面PQB,再由面面平行的判定定理,即可得到结论.
(2)连AC交BD于O,连MO,由三角形的中位线定理,可得PA∥OM,结合线面平行的判定定理,即可得到PA∥平面MBD;
(3)令N为AB中点,结合(1)中结论易得PQ⊥CN,又由正方形ABCD中Q,N分别为AD,AB中点,则CN⊥BQ,结合线面垂直的判定定理,可得CN⊥平面PQB,再由面面平行的判定定理,即可得到结论.
解答:解:(1)正△PAD中,Q为AD的中点
故PQ⊥AD
由
?PQ⊥平面ABCD.(3分)
∵Q∈平面ABCDPQ长为P到平面ABCD的距离.
因为AD=4,
所以PQ=2
所以,P平行ABCD的距离为2
(5分)
(2)证明:连AC交BD于O,连MO
则ABCD为正方形,
所以O为AC中点,M为PC中点,
所以MO∥AP,(7分)
又AP?平面MBD,MO?平面MBD,
则AP∥平面MBD.(10分)
(3)N为AB中点时,平面PCN⊥平面PQB.(11分)
证明如下:由(1)证明知PQ⊥平面ABCD,又CN?平面ABCD,则PQ⊥CN(12分)
又因为正方形ABCD中Q,N分别为AD,AB中点,则CN⊥BQ(13分)
∴CN⊥平面PQB(14分)
又∵CN?平面PCN
所以,平面PCN⊥平面PQB.(15分)
故PQ⊥AD
由
|
∵Q∈平面ABCDPQ长为P到平面ABCD的距离.
因为AD=4,
所以PQ=2
| 3 |
所以,P平行ABCD的距离为2
| 3 |
(2)证明:连AC交BD于O,连MO
则ABCD为正方形,
所以O为AC中点,M为PC中点,
所以MO∥AP,(7分)
又AP?平面MBD,MO?平面MBD,
则AP∥平面MBD.(10分)
(3)N为AB中点时,平面PCN⊥平面PQB.(11分)
证明如下:由(1)证明知PQ⊥平面ABCD,又CN?平面ABCD,则PQ⊥CN(12分)
又因为正方形ABCD中Q,N分别为AD,AB中点,则CN⊥BQ(13分)
∴CN⊥平面PQB(14分)
又∵CN?平面PCN
所以,平面PCN⊥平面PQB.(15分)
点评:本题考查的知识点是平面与平面垂直的判定与性质,直线与平面平行的判定,点到平面的距离,(1)中关键是证明PQ⊥平面ABCD,(2)关键在面内找到与已知直线平行的直线,(3)中关键是要找准N点的位置.

练习册系列答案
相关题目
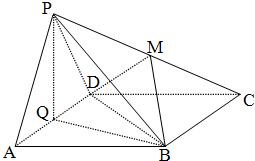 如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.
如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.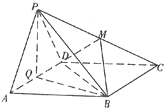 如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M、Q分别为PC,AD的中点.
如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M、Q分别为PC,AD的中点.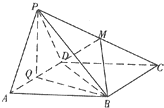 如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.
如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.