题目内容
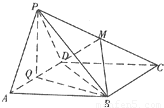
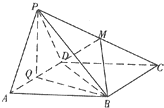 如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.
如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.(1)求证:PA∥平面MBD;
(2)求:A到平面PBD的距离.
分析:(1)连接AC交BD于O,再连接MO,根据中位线定理可得到PA∥MO,进而可根据线面平行的判定定理可证;
(2)作QE⊥BD,连接PE,计算PE的长,利用等体积,即可得到结论.
(2)作QE⊥BD,连接PE,计算PE的长,利用等体积,即可得到结论.
解答:(1)证明:连AC交BD于O,连MO,则ABCD为正方形,所以O为AC中点,M为PC中点,所以MO∥PA,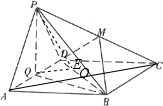
又PA?平面MBD,MO?平面MBD,∴PA∥平面MBD;
(2)解:作QE⊥BD,连接PE,则
∵正方形ABCD所在平面与正△PAD所在平面互相垂直,Q为AD的中点
∴PQ⊥平面ABCD
∵QE⊥BD,∴PE⊥BD,
∵正方形ABCD的边长为4,∴PQ=2
,QE=
,BD=4
,∴PE=
设A到平面PBD的距离为d,则由等体积可得
×
×4×4×2
=
×
×4
×
×d
∴d=
.

又PA?平面MBD,MO?平面MBD,∴PA∥平面MBD;
(2)解:作QE⊥BD,连接PE,则
∵正方形ABCD所在平面与正△PAD所在平面互相垂直,Q为AD的中点
∴PQ⊥平面ABCD
∵QE⊥BD,∴PE⊥BD,
∵正方形ABCD的边长为4,∴PQ=2
| 3 |
| 2 |
| 2 |
| 14 |
设A到平面PBD的距离为d,则由等体积可得
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 14 |
∴d=
4
| ||
| 7 |
点评:本题考查直线与平面平行的判定,考查点到平面的距离,正确运用等体积转化是关键.

练习册系列答案
相关题目
 如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.
如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.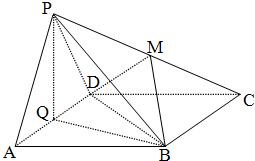 如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.
如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.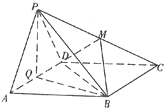 如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M、Q分别为PC,AD的中点.
如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M、Q分别为PC,AD的中点.