题目内容
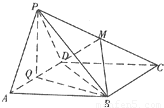
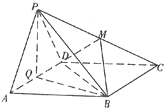 如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M、Q分别为PC,AD的中点.
如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M、Q分别为PC,AD的中点.(1)求证:PA∥平面MBD;
(2)求:二面角P-BD-A的余弦值;
(3)试问:在线段AB上是否存在一点N,使得平面PCN⊥平面PQB?若存在,试指出点N的位置,并证明你的结论;若不存在,请说明理由.
分析:(1)连接AC交BD于点O,连接MO,由正方形ABCD知O为AC的中点,由M为PC的中点,知MO∥PA,由此能够证明PA∥平面MBD
(2)以QA为x轴,过Q平行于AB的直线为y轴,以QP为z轴,建立空间直角坐标系,利用向量法能够求出二面角P-BD-A的余弦值.
(3)存在点N,当N为AB中点时,平面PQB⊥平面PNC.由四边形ABCD是正方形,Q为AD的中点,知BQ⊥NC,由此能够证明平面PCN⊥平面PQB.
(2)以QA为x轴,过Q平行于AB的直线为y轴,以QP为z轴,建立空间直角坐标系,利用向量法能够求出二面角P-BD-A的余弦值.
(3)存在点N,当N为AB中点时,平面PQB⊥平面PNC.由四边形ABCD是正方形,Q为AD的中点,知BQ⊥NC,由此能够证明平面PCN⊥平面PQB.
解答:(1)证明:连接AC交BD于点O,连接MO,
由正方形ABCD知O为AC的中点,
∵M为PC的中点,
∴MO∥PA,
∵MO?平面MBD,PA?平面MBD,
∴PA∥平面MBD
(2)解:以QA为x轴,过Q平行于AB的直线为y轴,以QP为z轴,建立空间直角坐标系,
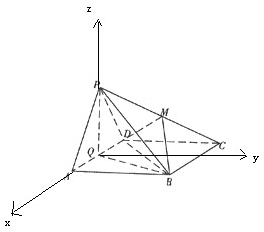
则P(0,0,2
),D(-2,0,0),B(2,4,0),
∴
=(2,0,2
),
=(4,4,0),
设平面PBD的法向量
=(x,y,z),则
•
=0,
•
=0,
∴
,∴
=(
,-
,-1),
∵平面ABD的法向量
=(0,0,1),
∴二面角P-BD-A的余弦值cosθ=|cos<
,
>|=|
|=
,
∴二面角P-BD-A的余弦值为
.
(3)解:存在点N,当N为AB中点时,平面PQB⊥平面PNC,
∵四边形ABCD是正方形,Q为AD的中点,∴BQ⊥NC.
由(1)知,PQ⊥平面ABCD,NC?平面ABCD,∴PQ⊥NC,
又BQ∩PQ=Q,∴NC⊥平面PQB,
∵NC?平面PCN,
∴平面PCN⊥平面PQB.
由正方形ABCD知O为AC的中点,
∵M为PC的中点,
∴MO∥PA,
∵MO?平面MBD,PA?平面MBD,
∴PA∥平面MBD
(2)解:以QA为x轴,过Q平行于AB的直线为y轴,以QP为z轴,建立空间直角坐标系,

则P(0,0,2
| 3 |
∴
| DP |
| 3 |
| DB |
设平面PBD的法向量
| n1 |
| DP |
| n1 |
| DB |
| n1 |
∴
|
| n1 |
| 3 |
| 3 |
∵平面ABD的法向量
| n2 |
∴二面角P-BD-A的余弦值cosθ=|cos<
| n1 |
| n2 |
| -1 | ||
|
| ||
| 7 |
∴二面角P-BD-A的余弦值为
| ||
| 7 |
(3)解:存在点N,当N为AB中点时,平面PQB⊥平面PNC,
∵四边形ABCD是正方形,Q为AD的中点,∴BQ⊥NC.
由(1)知,PQ⊥平面ABCD,NC?平面ABCD,∴PQ⊥NC,
又BQ∩PQ=Q,∴NC⊥平面PQB,
∵NC?平面PCN,
∴平面PCN⊥平面PQB.
点评:本题考查直线与平面平行的证明,考查二面角的求法,考查平面与平垂直的证明,解题时要认真审题,仔细解答,注意向量法和等价转化思想的合理运用.

练习册系列答案
相关题目
 如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.
如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.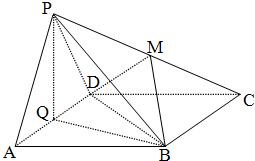 如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.
如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.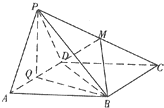 如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.
如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.