题目内容
解关于x的不等式x -(m+1)x+m>0
-(m+1)x+m>0
 -(m+1)x+m>0
-(m+1)x+m>0①当m>1时,上述不等式的解集为{x|x>m,或x<1};
②当m =1时,上述不等式可化为(x-1)2>0,∴x≠1,即解集为{x|x≠1};
③当m<1时,上述不等式的解集为{x|x>1,或x<m }.
②当m =1时,上述不等式可化为(x-1)2>0,∴x≠1,即解集为{x|x≠1};
③当m<1时,上述不等式的解集为{x|x>1,或x<m }.
试题分析:原不等式可化为 (x-m)(x-1)>0,由此求出它的解集.则结合二次函数图像以及函数的值的范围可知,满足不等式的解集为,解:∵x2-(1+m)x+ m>0,可化为(x-1)(x- m)>0.①当m>1时,上述不等式的解集为{x|x>m,或x<1};②当m =1时,上述不等式可化为(x-1)2>0,∴x≠1,即解集为{x|x≠1};③当m<1时,上述不等式的解集为{x|x>1,或x<m }.
点评:本题主要考查一元二次不等式的解法,属于基础题

练习册系列答案
相关题目
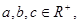 M=
M=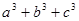 , N=
, N=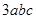 ,则M与N的大小关系为 .
,则M与N的大小关系为 . 的不等式
的不等式 (2)
(2) (3)
(3)
 中,三内角
中,三内角 、
、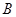 、
、 所对边的长分别为
所对边的长分别为 、
、 、
、 ,已知
,已知 ,则
,则 的解集为
的解集为 ,则
,则 ______.
______.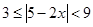
 的不等式
的不等式  ,
,
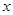 的不等式
的不等式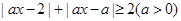 .
.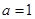 时,求此不等式的解集;
时,求此不等式的解集;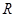 ,求实数
,求实数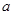 的取值范围.
的取值范围. .
. 的解集为
的解集为 ,求实数
,求实数 的值;
的值; 对一切实数
对一切实数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 则
则
 则
则
 则
则 则
则