题目内容
解关于 的不等式
的不等式
(1) (2)
(2) (3)
(3)
 的不等式
的不等式(1)
 (2)
(2) (3)
(3)
(1) ;
;
(2)当 时,原不等式无解
时,原不等式无解
当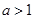 时原不等式解集{x|
时原不等式解集{x| }
}
当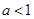 时原不等式解集{x|
时原不等式解集{x| };
};
(3){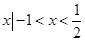 或
或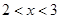 }。
}。
 ;
;(2)当
 时,原不等式无解
时,原不等式无解当
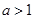 时原不等式解集{x|
时原不等式解集{x| }
}当
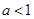 时原不等式解集{x|
时原不等式解集{x| };
};(3){
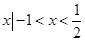 或
或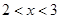 }。
}。试题分析:(1)原不等式变形:
 ,不等式解集为
,不等式解集为 4分
4分(2)原不等式变形:

①当
 时,原不等式无解
时,原不等式无解②当
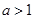 时,原不等式解集
时,原不等式解集
当
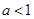 时,原不等式解集
时,原不等式解集
综上所述:当
 时,原不等式无解
时,原不等式无解当
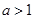 时原不等式解集
时原不等式解集
当
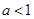 时原不等式解集
时原不等式解集 8分
8分(3)解:
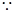
 即
即


 不等式解集为{
不等式解集为{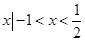 或
或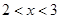 } 12分
} 12分点评:中档题,解一元二次不等式,首先选择“因式分解”法。涉及含参数不等式问题,要注意对参数加以讨论,或依据二次项系数,或根据根的大小比较,或根据判别式的取值,应做到不重不漏。

练习册系列答案
相关题目
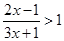 的解集是 。
的解集是 。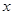 的不等式
的不等式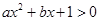 的解集是
的解集是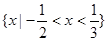 ,则
,则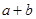 =_________
=_________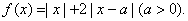
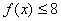 ;
;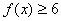 恒成立,求正实数a的取值范围。
恒成立,求正实数a的取值范围。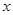 的不等式
的不等式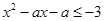 的解集不是空集,则实数
的解集不是空集,则实数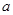 的取值范围是____.
的取值范围是____.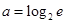 ,
,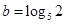 ,
,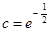 (其中
(其中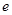 是自然对数的底),则( )
是自然对数的底),则( )



 对于
对于 恒成立,则实数
恒成立,则实数 的取值范围为( )
的取值范围为( )
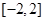


 -(m+1)x+m>0
-(m+1)x+m>0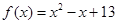 ,实数
,实数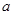 满足
满足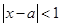 ,求证:
,求证: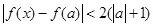 .
.