题目内容
已知数列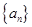 是首项
是首项 的等比数列,其前
的等比数列,其前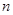 项和
项和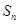 中,
中,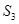 、
、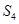 、
、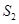 成等差数列.
成等差数列.
(1)求数列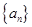 的通项公式;
的通项公式;
(2)设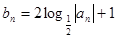 ,求数列{
,求数列{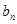 }的前
}的前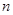 项和为
项和为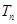 ;
;
(3)求满足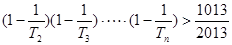 的最大正整数
的最大正整数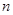 的值.
的值.
【答案】
(1)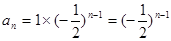
(2)
(3)最大正整数 的值为
的值为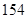 .
.
【解析】
试题分析:解:(1)若 ,则
,则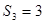 ,
,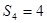 ,
,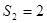 ,显然
,显然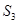 ,
,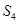 ,
,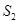 不构成等差数列,
不构成等差数列,
∴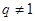 .
.
故由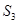 ,
,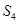 ,
,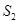 成等差数列得:
成等差数列得: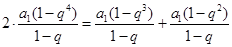 2分
2分
∴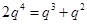
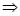
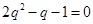
 ,
,
∵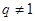 ,∴
,∴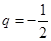 .
4分
.
4分
∴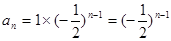 .
5分
.
5分
(2)∵
7分
∴ 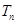 =
=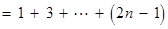

 .
9分
.
9分
(3)
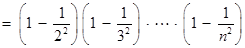
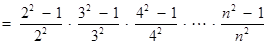
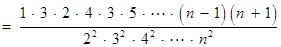 11分
11分
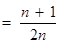 . 13分
. 13分
令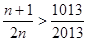 ,解得:
,解得: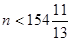 .
.
故满足条件的最大正整数 的值为
的值为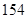 . 14分
. 14分
说明:以上各题只给出一种解(证)法,若还有其他解(证)法,请酌情给分。
考点:数列的通项公式以及求和
点评:主要是考查了数列的求和以及数列的通项公式的求解,属于基础题。

练习册系列答案
相关题目
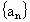 是首项a且公比q不等于1的等比数列,
是首项a且公比q不等于1的等比数列, 是其前n项和,
是其前n项和,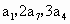 成等差数列.
成等差数列.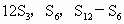 成等比数;
成等比数;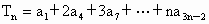 .
. 是首项为1,公差为
是首项为1,公差为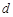 的等差数列,数列
的等差数列,数列 是首项为1,公比为
是首项为1,公比为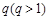 的等比
的等比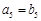 ,
,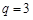 ,求数列
,求数列 的前
的前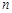 项和;
项和;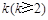 ,使得
,使得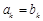 .试比较
.试比较 与
与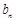 的大小,并说明理由.
的大小,并说明理由. =p(p为正常数,n∈N*),则称{an}为“等方比数列”.若数列{an}是等方比数列则数列{an}必是等比数列.
=p(p为正常数,n∈N*),则称{an}为“等方比数列”.若数列{an}是等方比数列则数列{an}必是等比数列.