题目内容
3.在对人们的休闲方式的一次调查中,共调查了100人,其中女性20人,男性80人.女性中有10人主要的休闲方式是看电视,另外10人主要的休闲方式是运动;男性中有20人主要的休闲方式是看电视,另外60人主要的休闲方式是运动.(1)根据以上数据建立一个2×2的列联表;
(2)能否在犯错误的概率不超过0.05的前提下认为性别与休闲方式有关系?
参考公式:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d
参考数据:
| P(k2>k) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
分析 (1)根据共调查了100人,其中女性20人,男性80人.女性中有10人主要的休闲方式是看电视,另外10人主要的休闲方式是运动;男性中有20人主要的休闲方式是看电视,另外60人主要的休闲方式是运动,得到列联表.
(2)根据列联表中所给的数据做出观测值,把观测值同临界值进行比较得到能在犯错误的概率不超过0.05的前提下认为性别与休闲方式有关系
解答 解:(1)根据所给的数据得到列联表
| 男 | 女 | 合计 | |
| 看电视 | 20 | 10 | 30 |
| 运动 | 60 | 10 | 70 |
| 合计 | 80 | 20 | 100 |
故能在犯错误的概率不超过0.05的前提下认为性别与休闲方式有关系.
点评 本题考查独立性检验的应用和列联表的做法,本题解题的关键是正确计算出这组数据的观测值,理解临界值对应的概率的意义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.sin$\frac{20π}{3}$=( )
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
15.因为对数函数y=logax是增函数(大前提),而是对数函数$y={log_{\frac{1}{3}}}x$(小前提),所以y=log${\;}_{\frac{1}{3}}$x是增函数(结论).这个推理过程中( )
| A. | 大前提错误导致结论错误 | |
| B. | 小前提错误导致结论错误 | |
| C. | 推理形式错误导致结论错误 | |
| D. | 大前提和小前提都错误导致结论错误 |
13.已知离散型随机变量X的分布列为P(X=1)=$\frac{3}{5}$,P(X=2)=$\frac{3}{10}$,P(X=3)=$\frac{1}{10}$,则X的数学期望E(X)=( )
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
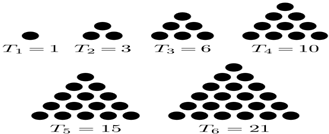 小毕喜欢把数描绘成沙滩上的小石子,他照如图所示摆成了正三角形图案,并把每个图案中总的石子个数叫做“三角形数”,记为Tn,则$\frac{1}{2{T}_{1}}$+$\frac{1}{2{T}_{2}}$+$\frac{1}{2{T}_{3}}$+…+$\frac{1}{2{T}_{2015}}$=$\frac{2015}{2016}$.
小毕喜欢把数描绘成沙滩上的小石子,他照如图所示摆成了正三角形图案,并把每个图案中总的石子个数叫做“三角形数”,记为Tn,则$\frac{1}{2{T}_{1}}$+$\frac{1}{2{T}_{2}}$+$\frac{1}{2{T}_{3}}$+…+$\frac{1}{2{T}_{2015}}$=$\frac{2015}{2016}$.