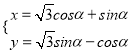题目内容
【题目】设平面向量 
=（cosx，sinx）， 
=（cosx+2 
，sinx）， 
=（sinα，cosα），x∈R．
（1）若 
，求cos（2x+2α）的值；
（2）若α=0，求函数f（x）= 
的最大值，并求出相应的x值．
【答案】
（1）
解：若 
，则 
=0，
∴cosxsinα+sinxcosα=0，
∴sin（x+α）=0，
∴cos（2x+2α）=1﹣2sin2（x+α）=1．
（2）
若α=0， =（0，1），
则f（x）= 
=（cosx，sinx）（cosx+2 
，sinx﹣2）=cosx（cosx+2 ）+sinx（sinx﹣2）=1﹣2sinx+2 cosx=1+4sin（x+ 
），
所以，f（x）max=5，x=2kπ﹣ 
（k∈Z）．
【解析】（1）利用两个向量垂直，它们的数量积等于0，以及二倍角的余弦公式求得cos（2x+2α）的值．（2）若α=0，则 =（0，1），由题意化简可得函数解析式：f（x）=1+4sin（x+ ），利用正弦函数的有界性求出函数的最值．
【考点精析】掌握两角和与差的余弦公式是解答本题的根本，需要知道两角和与差的余弦公式：
．
练习册系列答案
相关题目
