题目内容
在Rt△ABC中,AB=AC=1,如果椭圆经过A,B两点,它的一个焦点为C,另一个焦点在AB上,则这个椭圆的离心率为
-
-
.
| 6 |
| 3 |
| 6 |
| 3 |
分析:画出图形,利用椭圆的定义,求出三角形的周长,得到a的值,利用三角形的是直角三角形与椭圆的定义,求出c的值,推出椭圆的离心率.
解答: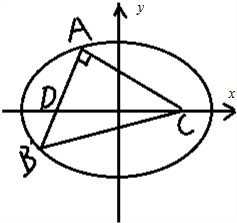 解:建立如图坐标系
解:建立如图坐标系
RT△ABC周长:4a,
4a=1+1+
=2+
则a=
,
记AB上的另一个焦点为D,
则AD=2a-AC=
,
在RT△ACD中,∠A=90°,AC=1,AD=
,
则2c=CD=
=
,
则c=
,
e=
=
=
-
.
故答案为:
-
.
 解:建立如图坐标系
解:建立如图坐标系RT△ABC周长:4a,
4a=1+1+
| 2 |
| 2 |
2+
| ||
| 4 |
记AB上的另一个焦点为D,
则AD=2a-AC=
| ||
| 2 |
在RT△ACD中,∠A=90°,AC=1,AD=
| ||
| 2 |
则2c=CD=
1+
|
| ||
| 2 |
则c=
| ||
| 4 |
e=
| c |
| a |
| ||||
|
| 6 |
| 3 |
故答案为:
| 6 |
| 3 |
点评:本题是基础题,考查椭圆的定义的应用,椭圆的离心率的求法,直角三角形的应用,考查计算能力.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
在Rt△ABC中,∠A=90°,|
|=1,则
•
的值为:( )
| AB |
| AB |
| BC |
| A、1 | B、-1 |
| C、1或-1 | D、不能确定 |
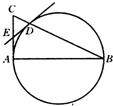 15、如图,在Rt△ABC中,∠A=90°,以AB为直径的半圆交BC于D,过D作圆的切线交AC于E.
15、如图,在Rt△ABC中,∠A=90°,以AB为直径的半圆交BC于D,过D作圆的切线交AC于E.