题目内容
在Rt△ABC中,a、b为直角边,c为斜边,则c的外接圆半径R=分析:这是直接考查直角三角形的性质,这些性质建议大家牢牢记住,考试的时候可以做为公式直接使用.(1)在Rt△ABC中,若a、b为直角边,c为斜边,外接圆的半径就是斜边的一半(2)内切圆半径和其三边的关系为:r=
(a+b-c);(3)斜边上的高hc=
’(4)斜边被垂足分成两线段之长分别为:
,
| 1 |
| 2 |
| a•b |
| c |
| a2 |
| C |
| b2 |
| C |
解答:解:在Rt△ABC中,若a、b为直角边,c为斜边,
外接圆的半径就是斜边的一半,故R=
;
内切圆半径和其三边的关系为:r=
(a+b-c);
斜边上的高hc=
(由面积公式不难证明)
斜边被垂足分成两线段之长分别为:
,
(由相似三角形性质或射影定理不难证明)
故答案为:
;
(a+b-c);
;
,
外接圆的半径就是斜边的一半,故R=
| c |
| 2 |
内切圆半径和其三边的关系为:r=
| 1 |
| 2 |
斜边上的高hc=
| a•b |
| c |
斜边被垂足分成两线段之长分别为:
| a2 |
| C |
| b2 |
| C |
故答案为:
| c |
| 2 |
| 1 |
| 2 |
| a•b |
| c |
| a2 |
| C |
| b2 |
| C |
点评:直角三角形是三角形中的特例,也是考试中最常出现的数学模型,故我们要熟练掌握其基本性质,包括本题中的结论及相关的命题和公式.

练习册系列答案
相关题目
在Rt△ABC中,∠A=90°,|
|=1,则
•
的值为:( )
| AB |
| AB |
| BC |
| A、1 | B、-1 |
| C、1或-1 | D、不能确定 |
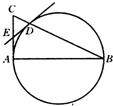 15、如图,在Rt△ABC中,∠A=90°,以AB为直径的半圆交BC于D,过D作圆的切线交AC于E.
15、如图,在Rt△ABC中,∠A=90°,以AB为直径的半圆交BC于D,过D作圆的切线交AC于E.