题目内容
9.已知数列{an}是首项为2,公差为-1的等差数列.令bn=($\frac{1}{2}$)${\;}^{{a}_{n}}$,求证数列{bn}是等比数列.并求其通项公式.分析 由题意写出等差数列的通项公式,得到an+1-an=-1,由等比数列的定义可证明数列{bn}是等比数列.代入等比数列的通项公式求得bn.
解答 证明:∵数列{an}是首项为2,公差为-1的等差数列,
∴an=2+(n-1)×(-1)=3-n,
∴an+1-an=3-(n+1)-3+n=-1.
则$\frac{{b}_{n+1}}{{b}_{n}}=\frac{(\frac{1}{2})^{{a}_{n+1}}}{(\frac{1}{2})^{{a}_{n}}}=(\frac{1}{2})^{{a}_{n+1}-{a}_{n}}$=$(\frac{1}{2})^{-1}=2$为常数.
又${b}_{1}=(\frac{1}{2})^{{a}_{1}}=(\frac{1}{2})^{2}=\frac{1}{4}$,
∴数列{bn}是以$\frac{1}{4}$为首项,以2为公比的等比数列.
∴${b}_{n}=\frac{1}{4}•{2}^{n-1}={2}^{n-3}$.
点评 本题考查等差数列的通项公式,考查了等比关系的确定,考查了等比数列的通项公式,是基础题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
14.若关于x的二次不等式ax2+bx+c≥0(a≠0)的解集是R,那么( )
| A. | a<0,且b2-4ac>0 | B. | a<0,且b2-4ac≤0 | C. | a>0,且b2-4ac≤0 | D. | a<0,且b2-4ac>0 |
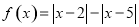 .
.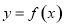 的值域;
的值域; 的解集.
的解集.