题目内容
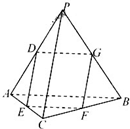 如图,在四面体PABC中,PC⊥AB,PA⊥BC,点D,E,F,G分别是棱AP,AC,BC,PB的中点.
如图,在四面体PABC中,PC⊥AB,PA⊥BC,点D,E,F,G分别是棱AP,AC,BC,PB的中点.(Ⅰ)求证:DE∥平面BCP;
(Ⅱ)求证:四边形DEFG为矩形;
(Ⅲ)是否存在点Q,到四面体PABC六条棱的中点的距离相等?说明理由.
分析:(I)根据两个点是两条边的中点,得到这条线是两条边的中位线,得到这条线平行于PC,根据线面平行的判定定理,得到线面平行.
(II)根据四个点是四条边的中点,得到中位线,根据中位线定理得到四边形是一个平行四边形,根据两条对角线垂直,得到平行四边形是一个矩形.
(III)做出辅助线,证明存在点Q到四面体PABC六条棱的中点的距离相等,根据第二问证出的四边形是矩形,根据矩形的两条对角线互相平分,又可以证出另一个矩形,得到结论.
(II)根据四个点是四条边的中点,得到中位线,根据中位线定理得到四边形是一个平行四边形,根据两条对角线垂直,得到平行四边形是一个矩形.
(III)做出辅助线,证明存在点Q到四面体PABC六条棱的中点的距离相等,根据第二问证出的四边形是矩形,根据矩形的两条对角线互相平分,又可以证出另一个矩形,得到结论.
解答:证明:(I)∵D,E分别为AP,AC的中点,
∴DE∥PC,
∵DE?平面BCP,
∴DE∥平面BCP.
(II)∵D,E,F,G分别为AP,AC,BC,PB的中点,
∴DE∥PC∥FG,DG∥AB∥EF
∴四边形DEFG为平行四边形,
∵PC⊥AB,
∴DE⊥DG,
∴四边形DEFG为矩形.
(III)存在点Q满足条件,理由如下:
连接DF,EG,设Q为EG的中点,
由(II)知DF∩EG=Q,且QD=QE=QF=QG=
EG,
分别取PC,AB的中点M,N,连接ME,EN,NG,MG,MN,
与(II)同理,可证四边形MENG为矩形,其对角线交点为EG的中点Q,
且QM=QN=
EG,
∴Q为满足条件的点.
∴DE∥PC,
∵DE?平面BCP,
∴DE∥平面BCP.
(II)∵D,E,F,G分别为AP,AC,BC,PB的中点,

∴DE∥PC∥FG,DG∥AB∥EF
∴四边形DEFG为平行四边形,
∵PC⊥AB,
∴DE⊥DG,
∴四边形DEFG为矩形.
(III)存在点Q满足条件,理由如下:
连接DF,EG,设Q为EG的中点,
由(II)知DF∩EG=Q,且QD=QE=QF=QG=
| 1 |
| 2 |
分别取PC,AB的中点M,N,连接ME,EN,NG,MG,MN,
与(II)同理,可证四边形MENG为矩形,其对角线交点为EG的中点Q,
且QM=QN=
| 1 |
| 2 |
∴Q为满足条件的点.
点评:本题考查直线与平面平行的判定,考查三角形中位线定理,考查平行四边形和矩形的判定及性质,本题是一个基础题.

练习册系列答案
相关题目
 (2012•广州一模)如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA、AC、CB、BP的中点.
(2012•广州一模)如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA、AC、CB、BP的中点.

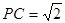 ,求四面体PABC的体积.
,求四面体PABC的体积. 如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA、AC、CB、BP的中点.
如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA、AC、CB、BP的中点. ,求四面体PABC的体积.
,求四面体PABC的体积.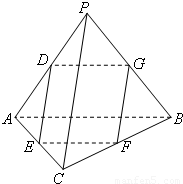 如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA、AC、CB、BP的中点.
如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA、AC、CB、BP的中点. ,求四面体PABC的体积.
,求四面体PABC的体积.