题目内容
如图,在四面体PABC中,PA、PB、PC两两垂直,∠PBA=45°,∠PBC=60°,M为AB的中点.
(1)求BC与平面PAB所成的角;
(2)求PC与平面ABC所成角的正弦值.
解析:(1)PC⊥面PAB,故BC与面PAB所成角等于∠CBP.即60°.
(2)∠PBA=45°,∠APB=90°,
∴△APB为等腰Rt△,M为AB中点.
∴PM⊥AB.PC⊥AB.
∴AB⊥面PMC.
面ABC⊥面PMC.∠PCM即为PC与面ABC所成角.
△PCM中,∠CPM=90°.sinPCM=![]() .设PB=a则PM=
.设PB=a则PM=![]() a,PC=
a,PC=![]() a,CM=
a,CM=
![]() a.
a.
∴sinPCM=![]() .
.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
 (2012•广州一模)如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA、AC、CB、BP的中点.
(2012•广州一模)如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA、AC、CB、BP的中点.
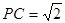 ,求四面体PABC的体积.
,求四面体PABC的体积. 如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA、AC、CB、BP的中点.
如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA、AC、CB、BP的中点. ,求四面体PABC的体积.
,求四面体PABC的体积.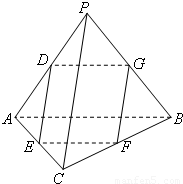 如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA、AC、CB、BP的中点.
如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA、AC、CB、BP的中点. ,求四面体PABC的体积.
,求四面体PABC的体积.