题目内容
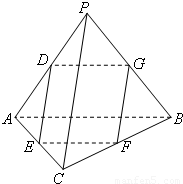 如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA、AC、CB、BP的中点.
如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA、AC、CB、BP的中点.(1)求证:D、E、F、G四点共面;
(2)求证:PC⊥AB;
(3)若△ABC和△PAB都是等腰直角三角形,且AB=2,
 ,求四面体PABC的体积.
,求四面体PABC的体积.
【答案】分析:(1)先利用三角形中位线定理和平行公理证明DG∥EF,从而利用平面的性质公理证明四点共面;
(2)取AB中点为O,先利用线面垂直的判定定理证明AB⊥面POC,再利用线面垂直的定义证明结论即可;
(3)先利用线面垂直的判定定理证明PO⊥面ABC,再利用棱锥体积计算公式计算体积即可
解答:解:(1)依题意DG∥AB,EF∥AB,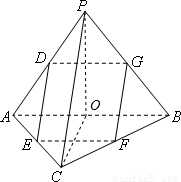
∴DG∥EF,
∴DG、EF共面,从而D、E、F、G四点共面.
(2)取AB中点为O,连接PO、CO
∵PA=PB,CA=CB,∴PO⊥AB,CO⊥AB,
∵PO∩CO=O,∴AB⊥面POC
∵PC?面POC,∴AB⊥PC
(3)因为△ABC和PAB是等腰直角三角形,所以 ,
,
∵ ,OP2+OC2=PC2,∴OP⊥OC,
,OP2+OC2=PC2,∴OP⊥OC,
又PO⊥AB,且AB∩OC=O,
∴PO⊥面ABC
∴
点评:本题主要考查了三棱锥中的线面关系和计算,线面垂直的判定和定义,平面的基本性质及其公理,三棱锥体积计算公式等知识
(2)取AB中点为O,先利用线面垂直的判定定理证明AB⊥面POC,再利用线面垂直的定义证明结论即可;
(3)先利用线面垂直的判定定理证明PO⊥面ABC,再利用棱锥体积计算公式计算体积即可
解答:解:(1)依题意DG∥AB,EF∥AB,

∴DG∥EF,
∴DG、EF共面,从而D、E、F、G四点共面.
(2)取AB中点为O,连接PO、CO
∵PA=PB,CA=CB,∴PO⊥AB,CO⊥AB,
∵PO∩CO=O,∴AB⊥面POC
∵PC?面POC,∴AB⊥PC
(3)因为△ABC和PAB是等腰直角三角形,所以
 ,
,∵
 ,OP2+OC2=PC2,∴OP⊥OC,
,OP2+OC2=PC2,∴OP⊥OC,又PO⊥AB,且AB∩OC=O,
∴PO⊥面ABC
∴

点评:本题主要考查了三棱锥中的线面关系和计算,线面垂直的判定和定义,平面的基本性质及其公理,三棱锥体积计算公式等知识

练习册系列答案
相关题目
 (2012•广州一模)如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA、AC、CB、BP的中点.
(2012•广州一模)如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA、AC、CB、BP的中点.

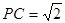 ,求四面体PABC的体积.
,求四面体PABC的体积. 如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA、AC、CB、BP的中点.
如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA、AC、CB、BP的中点. ,求四面体PABC的体积.
,求四面体PABC的体积.