题目内容
设函数f(x)=
（Ⅰ）在x=0，x=3处函数f（x）是否连续；
（Ⅱ）画出函数的图象；
（Ⅲ）求函数f（x）的连续区间．
|
（Ⅰ）在x=0，x=3处函数f（x）是否连续；
（Ⅱ）画出函数的图象；
（Ⅲ）求函数f（x）的连续区间．
分析：（Ⅰ）判定x=0，x=3处函数f（x）的左右极限存在且相等，即可得到结论；
（Ⅱ）分段作出函数图象，即可得到函数f（x）的图象；
（Ⅲ）由图象，可得函数的连续区间
（Ⅱ）分段作出函数图象，即可得到函数f（x）的图象；
（Ⅲ）由图象，可得函数的连续区间
解答：解：（Ⅰ）
f(x)=0，
f(x)=
x=0，∴
f(x)=0且f(0)=0，∴f（x）在x=0处连续，
同理f（x）在x=3处连续；…（4分）
（Ⅱ）图象如右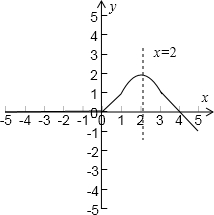
；…（8分）
（Ⅲ）连续区间为（-∞，+∞）．…（12分）
| lim |
| x→0- |
| lim |
| x→0+ |
| lim |
| x→0+ |
| lim |
| x→0 |
同理f（x）在x=3处连续；…（4分）
（Ⅱ）图象如右
；…（8分）（Ⅲ）连续区间为（-∞，+∞）．…（12分）
点评：本题考查函数的连续性，考查函数的图象，正确理解函数的连续性是关键．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
已知R为实数集，Q为有理数集．设函数f(x)=
，则（ ）
|
| A、函数y=f（x）的图象是两条平行直线 | ||||
B、
| ||||
| C、函数f[f（x）]恒等于0 | ||||
| D、函数f[f（x）]的导函数恒等于0 |
(0≤x＜1)的反函数为f-1(x),则…( )