题目内容
(文)已知R为实数集,Q为有理数集.设函数f(x)=
则( )
|
分析:根据分段函数的图象性质可知函数y=f(x)的图象是两条平行直线上的一些孤立的点,可判定A的真假;当x=1∈Q,-1∈Q,则由题意可得f(1)=f(-1)=1,不满足奇函数的定义f(-x)=-f(x);C若x是无理数,则f(x)=0,f[f(x)]=f(0)=1可判定C的真假,根据f[f(x)]=1可判定D的真假.
解答:解:A:函数y=f(x)的图象是两条平行直线上的一些孤立的点,故A错误
B:当x=1∈Q,-1∈Q,则由题意可得f(1)=f(-1)=1,不满足奇函数的定义f(-x)=-f(x),故B错误
C:若x是无理数,则f(x)=0,f[f(x)]=f(0)=1,故C不正确;
D:由f[f(x)]=1,可得函数f[f(x)]的导函数恒等于0,故D正确;
故选D.
B:当x=1∈Q,-1∈Q,则由题意可得f(1)=f(-1)=1,不满足奇函数的定义f(-x)=-f(x),故B错误
C:若x是无理数,则f(x)=0,f[f(x)]=f(0)=1,故C不正确;
D:由f[f(x)]=1,可得函数f[f(x)]的导函数恒等于0,故D正确;
故选D.
点评:本题主要考查了分段函数,以及函数奇偶性、图象、导数等有关问题,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
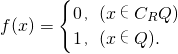 则
则