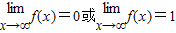题目内容
已知R为实数集,Q为有理数集.设函数f(x)=
,则( )
|
| A、函数y=f(x)的图象是两条平行直线 | ||||
B、
| ||||
| C、函数f[f(x)]恒等于0 | ||||
| D、函数f[f(x)]的导函数恒等于0 |
分析:根据分段函数的图象性质可知函数y=f(x)的图象是两条平行直线上的一些孤立的点,可判定A的真假,函数在∞处左右极限不等,则该函数不存在极限,可判定B的真假,若x是无理数,则f(x)=0,f[f(x)]=f(0)=1可判定C的真假,根据f[f(x)]=1可判定D的真假.
解答:解:函数y=f(x)的图象是两条平行直线上的一些孤立的点,故A不正确;
函数f(x)的极限只有唯一的值,左右极限不等,则该函数不存在极限,故B不正确;
若x是无理数,则f(x)=0,f[f(x)]=f(0)=1,故C不正确;
∵f[f(x)]=1,∴函数f[f(x)]的导函数恒等于0,故D正确;
故选D.
函数f(x)的极限只有唯一的值,左右极限不等,则该函数不存在极限,故B不正确;
若x是无理数,则f(x)=0,f[f(x)]=f(0)=1,故C不正确;
∵f[f(x)]=1,∴函数f[f(x)]的导函数恒等于0,故D正确;
故选D.
点评:本题主要考查了分段函数,以及函数极限、图象、导数等有关问题,属于中档题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
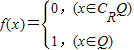 ,则( )
,则( )