题目内容
已知曲线C的参数方程为 (α∈R,α为参数).当极坐标系的极点与直角坐标系的原点重合,且极轴在x轴的正半轴上时,曲线D的极坐标力程为ρsin(θ+
(α∈R,α为参数).当极坐标系的极点与直角坐标系的原点重合,且极轴在x轴的正半轴上时,曲线D的极坐标力程为ρsin(θ+ )=
)=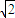 a.
a.(I)试将曲线C的方程化为普通方程,曲线D的方程化为直角坐标方程;
(II)试确定实数a的取值范围,使曲线C与曲线D有公共点.
【答案】分析:(I)先利用三角函数的同角公式展开曲线C的参数方程化成普通方程,再利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即可将曲线D的方程化为直角坐标方程.
(II)利用(1)中直角坐标方程,再利用圆心到直线的距离d≤r建立不等关系求出a的范围即可.
解答:解:(I)∵曲线C的参数方程是 (θ是参数),
(θ是参数),
∴消去参数得:x2+y2=1;,
∴曲线D的极坐标方程可写为ρsin(θ+ )=
)= a.
a.
即: ρsinθ+
ρsinθ+ ρcosθ=
ρcosθ=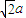 .
.
故直角坐标方程为:x+y-2a=0.
(II)利用圆心到直线的距离d≤r得
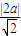 ≤1
≤1
解得:- ≤a≤
≤a≤ .
.
实数a的取值范围:- ≤a≤
≤a≤ .
.
点评:本题考查点的极坐标及参数方程和直角坐标的互化,能在极坐标系中用极坐标刻画点的位置,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互化.
(II)利用(1)中直角坐标方程,再利用圆心到直线的距离d≤r建立不等关系求出a的范围即可.
解答:解:(I)∵曲线C的参数方程是
 (θ是参数),
(θ是参数),∴消去参数得:x2+y2=1;,
∴曲线D的极坐标方程可写为ρsin(θ+
 )=
)= a.
a.即:
 ρsinθ+
ρsinθ+ ρcosθ=
ρcosθ=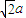 .
.故直角坐标方程为:x+y-2a=0.
(II)利用圆心到直线的距离d≤r得
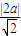 ≤1
≤1解得:-
 ≤a≤
≤a≤ .
.实数a的取值范围:-
 ≤a≤
≤a≤ .
.点评:本题考查点的极坐标及参数方程和直角坐标的互化,能在极坐标系中用极坐标刻画点的位置,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互化.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2012•湖南模拟)选做题(请考生在第16题的三个小题中任选两题作答,如果全做,则按前两题记分,要写出必要的推理与演算过程)
(2012•湖南模拟)选做题(请考生在第16题的三个小题中任选两题作答,如果全做,则按前两题记分,要写出必要的推理与演算过程) 附加题:(选做题:在下面A、B、C、D四个小题中只能选做两题)
附加题:(选做题:在下面A、B、C、D四个小题中只能选做两题)