题目内容
已知曲线C的参数方程为
(θ∈[0,π]),且点P(x,y)在曲线C上,则
的取值范围是( )
|
| y+x-1 |
| x |
分析:由题意得曲线C是半圆,借助已知动点在单位圆上任意动,而所求式子
=1+
,
的形式可以联想成在单位圆上动点P与点C(0,1)构成的直线的斜率,进而求解.
| y+x-1 |
| x |
| y-1 |
| x |
| y-1 |
| x |
解答: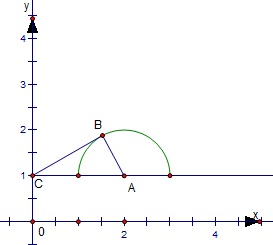 解:∵
解:∵
即
∴(x-2)2+(y-1)2=1,其中y∈[1,2]
由题意作出如下图形,
=1+
,
令k=
,则k可看作圆(x-2)2+y2=1上的动点P到点C(0,1)的连线的斜率而相切时的斜率,
由于此时直线与圆相切,
在直角三角形ACB中,∠ACB=30°,⇒k=
由图形知,k的取值范围是[0,
].
则
的取值范围是[1,1+
].
故选B.
 解:∵
解:∵
|
|
∴(x-2)2+(y-1)2=1,其中y∈[1,2]
由题意作出如下图形,
| y+x-1 |
| x |
| y-1 |
| x |
令k=
| y-1 |
| x |
由于此时直线与圆相切,
在直角三角形ACB中,∠ACB=30°,⇒k=
| ||
| 3 |
由图形知,k的取值范围是[0,
| ||
| 3 |
则
| y+x-1 |
| x |
| ||
| 3 |
故选B.
点评:此题重点考查了已知两点坐标写斜率,及直线与圆的相切与相交的关系,还考查了利用几何思想解决代数式子的等价转化的思想.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 (2012•湖南模拟)选做题(请考生在第16题的三个小题中任选两题作答,如果全做,则按前两题记分,要写出必要的推理与演算过程)
(2012•湖南模拟)选做题(请考生在第16题的三个小题中任选两题作答,如果全做,则按前两题记分,要写出必要的推理与演算过程) 附加题:(选做题:在下面A、B、C、D四个小题中只能选做两题)
附加题:(选做题:在下面A、B、C、D四个小题中只能选做两题)