题目内容
6.三棱锥P-ABC中,△ABC为等边三角形,PA=PB=PC=2,PA⊥PB,三棱锥P-ABC的外接球的表面积为( )| A. | 48π | B. | 12π | C. | 4$\sqrt{3}$π | D. | 32$\sqrt{3}$π |
分析 证明PA⊥PC,PB⊥PC,以PA、PB、PC为过同一顶点的三条棱,作长方体如图,则长方体的外接球同时也是三棱锥P-ABC外接球.算出长方体的对角线即为球直径,结合球的表面积公式,可算出三棱锥P-ABC外接球的表面积.
解答 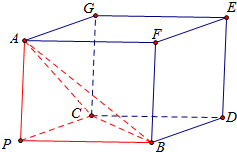 解:∵三棱锥P-ABC中,△ABC为等边三角形,PA=PB=PC=2,
解:∵三棱锥P-ABC中,△ABC为等边三角形,PA=PB=PC=2,
∴△PAB≌△PAC≌△PBC
∵PA⊥PB,
∴PA⊥PC,PB⊥PC
以PA、PB、PC为过同一顶点的三条棱,作长方体如图
则长方体的外接球同时也是三棱锥P-ABC外接球.
∵长方体的对角线长为$\sqrt{4+4+4}$=2$\sqrt{3}$,
∴球直径为2$\sqrt{3}$,半径R=$\sqrt{3}$,
因此,三棱锥P-ABC外接球的表面积是4πR2=4π×($\sqrt{3}$)2=12π
故选:B.
点评 本题给出三棱锥的三条侧棱两两垂直,求它的外接球的表面积,着重考查了长方体对角线公式和球的表面积计算等知识,属于基础题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
16.下列说法正确的是( )
| A. | “若$x=\frac{π}{3}$,则$sinx=\frac{{\sqrt{3}}}{2}$”的逆命题为真 | |
| B. | a,b,c为实数,若a>b,则ac2>bc2 | |
| C. | 命题p:?x∈R,使得x2+x-1<0,则?p:?x∈R,使得x2+x-1>0 | |
| D. | 若命题?p∧q为真,则p假q真 |
14.已知i为虚数单位,复数z=(1-i)(1+i)的模|z|的值是( )
| A. | 4 | B. | 2 | C. | 4i | D. | 2i |
 如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为棱PC上的动点,且$\frac{PM}{PC}$=λ(λ∈[0,1]).
如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为棱PC上的动点,且$\frac{PM}{PC}$=λ(λ∈[0,1]). 如图所示,AB为圆O的直径,BC,CD为圆O的切线,B,D为切点.
如图所示,AB为圆O的直径,BC,CD为圆O的切线,B,D为切点.