题目内容
在△ABC中,角A,B,C的对边分别为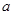 ,
, ,
, ,且
,且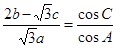 .
.
(1)求角 的值;
的值;
(2)若角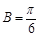 ,
, 边上的中线
边上的中线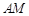 =
=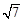 ,求
,求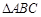 的面积.
的面积.
(1)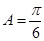 ;(2)
;(2)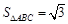 .
.
解析试题分析:(1)首先可将条件中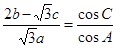 变形为
变形为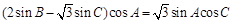 ,再利用正弦定理进行边角互化可得
,再利用正弦定理进行边角互化可得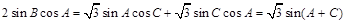 ,再由
,再由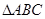 中
中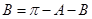 ,可将等式继续化简为
,可将等式继续化简为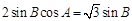 ,从而
,从而 ;(2)由(1)及条件
;(2)由(1)及条件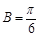 可得
可得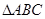 是等腰三角形,从而
是等腰三角形,从而 ,再由
,再由 边上的中线
边上的中线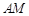 =
=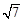 ,若设
,若设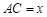 ,则
,则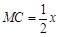 ,可考虑在
,可考虑在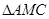 中采用余弦定理,即有
中采用余弦定理,即有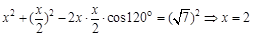 ,
,
从而可进一步求得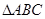 的面积:
的面积: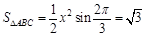 .
.
试题解析:(1)∵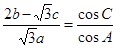 ,∴
,∴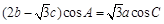 ,
,
由正弦定理得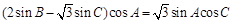 , 2分
, 2分
即 , 4分
, 4分
∵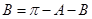 ,∴
,∴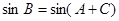 ,∴
,∴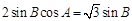 ,
,
又∵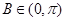 ,∴
,∴ ,∴
,∴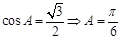 ; 7分
; 7分
(2)由(1)知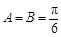 ,∴
,∴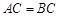 ,
,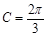 , 8分
, 8分
设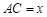 ,则
,则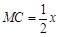 ,又∵
,又∵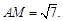
在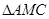 中,由余弦定理:
中,由余弦定理:
得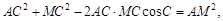 即
即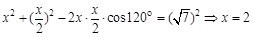 , 12分
, 12分
故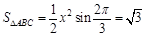 . 14分
. 14分
考点:1.三角恒等变形;2.正余弦定理解三角形.

练习册系列答案
相关题目
 .
. ,求△ABC的周长L的取值范围.
,求△ABC的周长L的取值范围. 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, .
. ,求角
,求角 ,
, ,且△
,且△ ,求
,求 其中
其中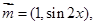
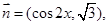 在
在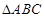 中,
中,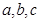 分别是角的对边,且
分别是角的对边,且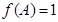 .
.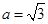 ,
,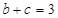 ,求
,求 、
、 、
、 分别是
分别是 的三个内角
的三个内角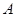 、
、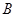 、
、 所对的边
所对的边 求
求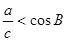 ,试判断
,试判断 两地连线上的定点
两地连线上的定点 处建造广告牌
处建造广告牌 ,其中
,其中 为顶端,
为顶端, 长35米,
长35米, 长80米,设
长80米,设 和
和 看
看 .
.
 ,问
,问 求
求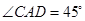 ,求建筑物AB和CD底部之间的距离BD。
,求建筑物AB和CD底部之间的距离BD。
 中,角
中,角 的对边分别为
的对边分别为 ,且
,且 .
.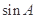 的值;
的值; ,
, ,求向量
,求向量 在
在 方向上的投影.
方向上的投影. ,
,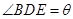 ,
,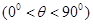 .
.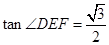 时,求
时,求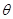 的大小;
的大小;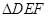 的面积S的最小值及使得S取最小值时
的面积S的最小值及使得S取最小值时