题目内容
8.直线l与两条直线x-y-7=0,y=1分别交于P、Q两点,线段PQ的中点为(1,-1),则直线l的斜率为-$\frac{2}{3}$.分析 根据中点坐标公式以及直线的斜率公式求出直线的斜率即可.
解答 解:设P(x0,y0),Q(a,1),PQ中点为M,
根据中点坐标公式得:$\frac{{x}_{0}+a}{2}$=1,$\frac{{y}_{0}+1}{2}$=-1
解得y0=-3,
∵P点在x-y-7=0上,
解得x0=4,a=-2;
∴P点坐标为(4,-3),Q点坐标为(-2,1);
∴由斜率公式k=$\frac{1{-y}_{0}}{a{-x}_{0}}$=$\frac{1-(-3)}{-2-4}$,得:k=-$\frac{2}{3}$,
故答案为:-$\frac{2}{3}$.
点评 本题考查直线的斜率,着重考查中点坐标公式的应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.$\frac{\sqrt{3}}{cos10°}$-$\frac{1}{sin170°}$=( )
| A. | -2 | B. | 2 | C. | 4 | D. | -4 |
16.如图,四面体ABCD中,各棱相等,M是CD的中点,则直线BM与平面ABC所成角的正弦值为( )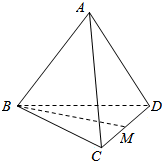

| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{2}}}{3}$ |
3.函数f(x)=log2(4-x2)定义域为( )
| A. | [-2,2] | B. | (-2,2) | C. | (-∞,2)∪(2,+∞) | D. | (-∞,2]∪[2,+∞) |
20.下列函数中,在区间(0,1)上是增函数的是( )
| A. | y=3-x | B. | y=x | C. | y=$\frac{1}{x}$ | D. | y=-x2 |