题目内容
18.若正方体的体对角线长是4,则正方体的体积是$\frac{64\sqrt{3}}{9}$.分析 根据体对角线与边长的关系求出正方体边长,代入体积公式计算.
解答 解:设正方体边长为a,则$\sqrt{{a}^{2}+{a}^{2}+{a}^{2}}$=4,
解得a=$\frac{4\sqrt{3}}{3}$,
∴V=a3=$\frac{64\sqrt{3}}{9}$.
点评 本题考查了正方体得体积计算,找到边长与对角线的关系是解题关键.

练习册系列答案
相关题目
8.设θ∈(0,$\frac{π}{4}$),则二次曲线$\frac{{x}^{2}}{tanθ}$-tanθ•y2=1的离心率的取值范围为( )
| A. | (1,$\sqrt{2}$] | B. | ($\frac{1}{2}$,$\frac{\sqrt{2}}{2}$) | C. | (1,$\sqrt{2}$) | D. | ($\sqrt{2}$,+∞) |
13.下列四个函数中,在(-∞,0)上是增函数的为( )
| A. | f(x)=x2+4 | B. | f(x)=3-$\frac{2}{x}$ | C. | f(x)=x2-5x-6 | D. | f(x)=1-x |
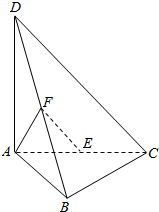 四面体ABCD中,AD⊥平面ABC,AB⊥BC,E,F分别为AC,BD的中点,AB=AD=2,∠BAC=60°.
四面体ABCD中,AD⊥平面ABC,AB⊥BC,E,F分别为AC,BD的中点,AB=AD=2,∠BAC=60°.