题目内容
【题目】一个盒子中装有2个红球，4个白球，除颜色外，它们的形状、大小、质量等完全相同.
（1）采用不放回抽样，先后取两次，每次随机取一个球，求恰好取到1个红球，1个白球的概率；
（2）采用放回抽样，每次随机取一球，连续取5次，求恰有两次取到红球的概率．
【答案】
（1）解：记“第i次取到红球”为Ai（i=1，2），
则先后取一球，恰好摸到一个红球和一个白球可表示为 
+ 
，
其概率为P（ + ）=P（ ）+P（ ）= 
，
∴恰好取到1个红球，1个白球的概率为 
（2）解：采用放回抽样，每次取到红球的概率 
．
连续取5次，可看作5次独立重复试验，
∴恰有两次取到红球的概率为 
【解析】（1）记“第i次取到红球”为Ai（i=1，2），则先后取一球，恰好摸到一个红球和一个白球可表示为 + ，由此能求出恰好取到1个红球，1个白球的概率．（2）采用放回抽样，每次取到红球的概率 ，连续取5次，可看作5次独立重复试验，由此能求出恰有两次取到红球的概率．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
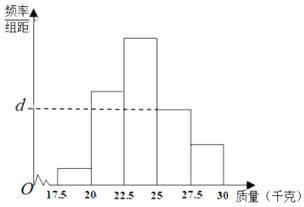
【题目】为了检测某种产品的质量（单位：千克），抽取了一个容量为N的样本，整理得到的数据作出了频率分布表和频率分布直方图如图：
分组 | 频数 | 频率 |
[17.5，20） | 10 | 0.05 |
[20，225） | 50 | 0.25 |
[22.5，25） | a | b |
[25，27.5） | 40 | c |
[27.5，30] | 20 | 0.10 |
合计 | N | 1 |
（Ⅰ）求出表中N及a，b，c的值；
（Ⅱ）求频率分布直方图中d的值；
（Ⅲ）从该产品中随机抽取一件，试估计这件产品的质量少于25千克的概率．
