题目内容
函数f(x)=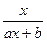 (a,b是非零实常数),满足f(2)=1,且方程f(x)=x有且仅有一个解。
(a,b是非零实常数),满足f(2)=1,且方程f(x)=x有且仅有一个解。
(1)求a、b的值;
(2)是否存在实常数m,使得对定义域中任意的x,f(x)+f(m–x)=4恒成立?为什么?
(3)在直角坐标系中,求定点A(–3,1)到此函数图象上任意一点P的距离|AP|的最小值。
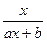 (a,b是非零实常数),满足f(2)=1,且方程f(x)=x有且仅有一个解。
(a,b是非零实常数),满足f(2)=1,且方程f(x)=x有且仅有一个解。(1)求a、b的值;
(2)是否存在实常数m,使得对定义域中任意的x,f(x)+f(m–x)=4恒成立?为什么?
(3)在直角坐标系中,求定点A(–3,1)到此函数图象上任意一点P的距离|AP|的最小值。
(1)1;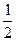 (2)
(2)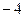 (3)3
(3)3
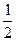 (2)
(2)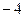 (3)3
(3)3(1)由f(2)=1得2a+b=2,又x=0一定是方程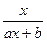 =x的解,
=x的解,
所以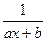 =1无解或有解为0,若无解,则ax+b=1无解,得a=0,矛盾,若有解为0,则b=1,所以a=
=1无解或有解为0,若无解,则ax+b=1无解,得a=0,矛盾,若有解为0,则b=1,所以a=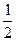 。
。
(2)f(x)=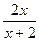 ,设存在常数m,使得对定义域中任意的x,f(x)+f(m–x)=4恒成立,
,设存在常数m,使得对定义域中任意的x,f(x)+f(m–x)=4恒成立,
取x=0,则f(0)+f(m–0)=4,即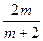 =4,m= –4(必要性),
=4,m= –4(必要性),
又m= –4时,f(x)+f(–4–x)=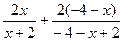 =……=4成立(充分性) ,所以存在常数m= –4,使得对定义域中任意的x,f(x)+f(m–x)=4恒成立,
=……=4成立(充分性) ,所以存在常数m= –4,使得对定义域中任意的x,f(x)+f(m–x)=4恒成立,
(3)|AP|2=(x+3)2+(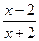 )2,设x+2=t,t≠0,
)2,设x+2=t,t≠0,
则|AP|2=(t+1)2+(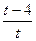 )2=t2+2t+2–
)2=t2+2t+2–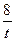 +
+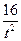 =(t2+
=(t2+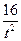 )+2(t–
)+2(t–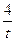 )+2=(t–
)+2=(t–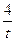 )2+2(t–
)2+2(t–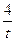 )+10
)+10
="(" t–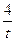 +1)2+9,所以当t–
+1)2+9,所以当t–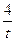 +1=0时即t=
+1=0时即t=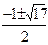 ,也就是x=
,也就是x=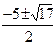 时,|AP| min =" 3" 。
时,|AP| min =" 3" 。
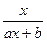 =x的解,
=x的解,所以
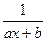 =1无解或有解为0,若无解,则ax+b=1无解,得a=0,矛盾,若有解为0,则b=1,所以a=
=1无解或有解为0,若无解,则ax+b=1无解,得a=0,矛盾,若有解为0,则b=1,所以a=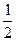 。
。(2)f(x)=
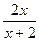 ,设存在常数m,使得对定义域中任意的x,f(x)+f(m–x)=4恒成立,
,设存在常数m,使得对定义域中任意的x,f(x)+f(m–x)=4恒成立,取x=0,则f(0)+f(m–0)=4,即
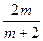 =4,m= –4(必要性),
=4,m= –4(必要性),又m= –4时,f(x)+f(–4–x)=
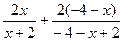 =……=4成立(充分性) ,所以存在常数m= –4,使得对定义域中任意的x,f(x)+f(m–x)=4恒成立,
=……=4成立(充分性) ,所以存在常数m= –4,使得对定义域中任意的x,f(x)+f(m–x)=4恒成立,(3)|AP|2=(x+3)2+(
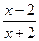 )2,设x+2=t,t≠0,
)2,设x+2=t,t≠0,则|AP|2=(t+1)2+(
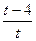 )2=t2+2t+2–
)2=t2+2t+2–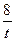 +
+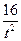 =(t2+
=(t2+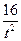 )+2(t–
)+2(t–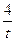 )+2=(t–
)+2=(t–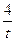 )2+2(t–
)2+2(t–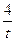 )+10
)+10="(" t–
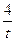 +1)2+9,所以当t–
+1)2+9,所以当t–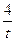 +1=0时即t=
+1=0时即t=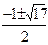 ,也就是x=
,也就是x=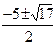 时,|AP| min =" 3" 。
时,|AP| min =" 3" 。
练习册系列答案
相关题目
 ,
, ,
,
 ,并猜想
,并猜想
 ,进一步归纳出更一般的结论
,进一步归纳出更一般的结论 则 ( )
则 ( )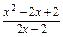 的最大值.
的最大值.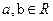 ,已知命题
,已知命题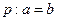 ;命题
;命题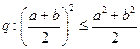 ,则
,则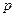 是
是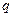 成立的
成立的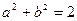 ,则
,则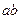 的最大值为_________
的最大值为_________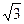 ,则2a+b+c的最小值为( )
,则2a+b+c的最小值为( ) 则每两客车营运多少年,其运营的年平均利润最大 ( )
则每两客车营运多少年,其运营的年平均利润最大 ( )